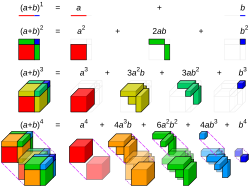
Binomial expansion

Binomial expansion uses an expression to make a series. It uses a bracket expression like [math]\displaystyle{ (x+y)^n }[/math]. There are three binomial expansions.

The formulas

There are basically three binomial expansion formulas:

[math]\displaystyle{ (a+b)^2 = a^2 + 2 ab + b^2 }[/math]		1st (Plus)
[math]\displaystyle{ (a-b)^2 = a^2 - 2 ab + b^2 }[/math]		2nd (Minus)
[math]\displaystyle{ (a+b) \cdot (a-b) = a^2 - b^2 }[/math]		3rd (Plus-Minus)

We can explain why there are such 3 formulas with a simple expansion of the product:

[math]\displaystyle{ (a+b)^2=(a+b)\cdot(a+b)=a \cdot a+a \cdot b+b \cdot a+b \cdot b=a^2+2 \cdot a \cdot b+b^2 }[/math]

[math]\displaystyle{ (a-b)^2=(a-b) \cdot (a-b)=a \cdot a-a \cdot b-b \cdot a+b \cdot b=a^2-2 \cdot a \cdot b+b^2 }[/math]

[math]\displaystyle{ (a+b) \cdot (a-b)=a \cdot a-a \cdot b+b \cdot a-b \cdot b=a^2-b^2 }[/math]

Using Pascal's triangle

If [math]\displaystyle{ n }[/math] is an integer ([math]\displaystyle{ n \in \mathbb{Z} }[/math]), we use Pascal's triangle.

To expand [math]\displaystyle{ (x+y)^2 }[/math]:

• find row 2 of Pascal's triangle (1, 2, 1)
• expand [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] so the [math]\displaystyle{ x }[/math] power goes down by 1 each time from [math]\displaystyle{ n }[/math] to 0 and the [math]\displaystyle{ y }[/math] power goes up by 1 each time from 0 up to [math]\displaystyle{ n }[/math]
• times the numbers from Pascal's triangle with the right terms.

So [math]\displaystyle{ (x+y)^2 = 1x^2y^0 + 2x^1y^1 + 1x^0y^2 }[/math]

For example:

[math]\displaystyle{ (3+2x)^2 = 1 \cdot 3^2 \cdot (2x)^0 + 2 \cdot 3^1 \cdot (2x)^1 + 1 \cdot 3^0 \cdot (2x)^2 = 9 + 12x + 4x^2 }[/math]

So as a rule:

[math]\displaystyle{ (x+y)^n = a_0x^ny^0 + a_1x^{n-1}y^1+ a_2x^{n-2}y^2+ \cdots + a_{n-1}x^{1}y^{n-1}+ a_nx^0y^n }[/math]

where [math]\displaystyle{ a_i }[/math] is the number at row [math]\displaystyle{ n }[/math] and position [math]\displaystyle{ i }[/math] in Pascal's triangle.

Examples

[math]\displaystyle{ (5+3x)^3 = 1 \cdot 5^3 \cdot (3x)^0 + 3 \cdot 5^2 \cdot (3x)^1 + 3 \cdot 5^1 \cdot (3x)^2 + 1 \cdot 5^0 \cdot (3x)^3 }[/math]

[math]\displaystyle{ = 125 + 75 \cdot 3x + 15 \cdot 9x^2 + 1 \cdot 27x^3 = 125 + 225x + 135x^2 + 27x^3 }[/math]

[math]\displaystyle{ (5-3x)^3 = 1 \cdot 5^3 \cdot (-3x)^0 + 3 \cdot 5^2 \cdot (-3x)^1 + 3 \cdot 5^1 \cdot (-3x)^2 + 1 \cdot 5^0 \cdot (-3x)^3 }[/math]

[math]\displaystyle{ = 125 + 75 \cdot (-3x) + 15 \cdot 9x^2 + 1 \cdot (-27x^3) = 125 - 223x + 135x^2 - 27x^3 }[/math]

[math]\displaystyle{ (7+4x^2)^5 = 1 \cdot 7^5 \cdot (4x^2)^0 + 5 \cdot 7^4 \cdot (4x^2)^1 + 10 \cdot 7^3 \cdot (4x^2)^2 + 10 \cdot 7^2 \cdot (4x^2)^3 + 5 \cdot 7^1 \cdot (4x^2)^4 + 1 \cdot 7^0 \cdot (4x^2)^5 }[/math]

[math]\displaystyle{ = 16807 + 12005 \cdot 4x^2 + 3430 \cdot 16x^4 + 490 \cdot 64x^6 + 35 \cdot 256x^8 + 1 \cdot 1024x^{10} }[/math]

[math]\displaystyle{ \, = 16807 + 48020x^2 + 54880x^4 + 31360x^6 + 8960x^8 + 1024x^{10} }[/math]