Centripetal force
_a.jpg)
Centripetal acceleration is a force that acts on a body that revolves around a centre of a circular path. This force keeps the body in circular motion. Newton's first law is that a moving object will continue in its motion in a straight path unless acted on by an external force.
When you hold a rope with an object attached to it, and spin it in a circular motion around the hand of the person holding the rope, the rope becomes tight and keeps the body from flying away. This force acts towards the center of motion, not away from it.
An object changes direction, but may maintain a constant speed, if acted upon by a centripetal acceleration. In such a case, we know from its angular frequency that [math]\displaystyle{ v = \omega r }[/math]. From Newton's second law we know that force equals mass times acceleration. Here acceleration is the negative of the radius coming from the centre of the circular motion. [math]\displaystyle{ F_r = ma_r =-mv^2 \frac{\vec{\mathbf{r}}}{r^2} = -\frac{mv^2}{r} \hat\mathbf{r} }[/math]
In this formula, think that the centripetal force and the centripetal momentum are the same thing because they are both measured in Newtons.
If, however, the angular frequency is not constant (as might be the case in a roller-coaster ride) then [math]\displaystyle{ \omega }[/math] does vary with respect to time. Here
[math]\displaystyle{ \frac{d \omega}{dt} = \frac{d^2 \theta}{d \theta^2} =\frac{1}{r} \frac{dv}{dt} }[/math]
Thus
[math]\displaystyle{ r = \frac{s}{\theta} = \frac{dv}{d\omega} }[/math]
as [math]\displaystyle{ \omega = \frac{d \theta}{d t} }[/math] and [math]\displaystyle{ s = r \theta }[/math] , which we know from the angular frequency.
Geometric proof for uniform circular motion
In the figure to the right we define the displacement vector [math]\displaystyle{ \vec s }[/math] to represent motion in a circle. The magnitude of [math]\displaystyle{ \vec s }[/math] is denoted as [math]\displaystyle{ R\equiv ||\vec s|| }[/math] and represents the radius of the particle's orbit.
Centripetal Force Media
A particle is disturbed from its uniform linear motion by a series of short kicks (1, 2, …), giving its trajectory a nearly circular shape. The force is referred to as a centripetal force in the limit of a continuously acting force directed towards the center of curvature of the path.
Velocity and acceleration in uniform circular motion
A body experiencing uniform circular motion requires a centripetal force, towards the axis as shown, to maintain its circular path.
Vector relationships for uniform circular motion; vector Ω representing the rotation is normal to the plane of the orbit with polarity determined by the right-hand rule and magnitude dθ /dt.
Upper panel: Ball on a banked circular track moving with constant speed v; Lower panel: Forces on the ball
/ R.
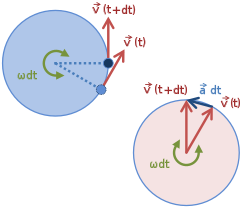
Polar unit vectors at two times t and t + dt for a particle with trajectory r ( t ); on the left the unit vectors uρ and uθ at the two times are moved so their tails all meet, and are shown to trace an arc of a unit radius circle. Their rotation in time dt is dθ, just the same angle as the rotation of the trajectory r ( t ).
