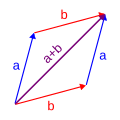
Commutative property
The commutative property says that the order of the numbers when adding or multiplying can be changed without changing the answer. For example, both [math]\displaystyle{ 2+8 }[/math] and [math]\displaystyle{ 8+2 }[/math] are equal to 10, and both [math]\displaystyle{ 5*7 }[/math] and [math]\displaystyle{ 7*5 }[/math] are equal to 35. This can be done with any numbers, or with more than two numbers.
Definition
The definition of commutative property of addition is [math]\displaystyle{ a+b=b+a }[/math]. a and b are variables and can be any number.
Some operations like dividing are not commutative. For instance, [math]\displaystyle{ 6\div3 }[/math] is 2, but [math]\displaystyle{ 3\div6 }[/math] is [math]\displaystyle{ \frac{1}{2} }[/math]. Subtraction is not commutative either: [math]\displaystyle{ 6-2 }[/math] is 4, but [math]\displaystyle{ 2-6 }[/math] is negative 4.
Higher mathematics
In higher mathematics like calculus, there are other commutative operations besides adding and multiplying. Commutative property must hold for each two elements of an Abelian group.