Conditional probability
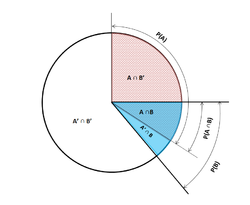
In probability theory, conditional probability is the probability of an event occurring, given that another event has occurred. Usually this is written as [math]\displaystyle{ P(A\mid B) }[/math]. This is read as "probability of A given B". The two events need not be related. They also need not occur at the same time. In the most general case,
[math]\displaystyle{ P(A\mid B) = \frac{P(A\cap B)}{P(B)} }[/math]
Expressed in words: The conditional probability of A occurring given B is the probability of both events occurring, divided by the probability of B occurring. As a division by zero is not defined, the probability of B occurring must not be zero.
Conditional Probability Media
Illustration of conditional probabilities with an Euler diagram. The unconditional probability P(A) = 0.30 + 0.10 + 0.12 = 0.52. However, the conditional probability P(A|B1) = 1, P(A|B2) = 0.12 ÷ (0.12 + 0.04) = 0.75, and P(A|B3) = 0.
On a tree diagram, branch probabilities are conditional on the event associated with the parent node. (Here, the overbars indicate that the event does not occur.)
Venn Pie Chart describing conditional probabilities
B) = P(BĀ) P(Ā)P(B) etc.
