Hooke's law
It is a law of mechanics and physics discovered by Robert Hooke.
This theory of elasticity says the extension of a spring is proportional to the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law is useful are known as linear-elastic or "Hookean" materials.
The spring equation
The length of a spring always changes by the same amount when it is pushed or pulled. The equation for this is:
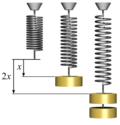
- [math]\displaystyle{ F=kx }[/math]
- where
- F is how much (push or pull) is on the spring
- k is a constant, the stiffness of the spring.
- x is how far the spring was pushed or pulled
When x = 0, the spring is at the equilibrium position. This equation only works on a linear spring. A linear spring is a spring that is only being pushed or pulled in one direction, such as left or right or up or down.
Elastic potential energy
Examples of everyday objects that have elastic potential energy are stretched or compressed elastic bands, springs, bungee cords, car shock absorbers, etc.
Elastic potential energy is the energy saved in an object that is stretched, compressed (compression is pressing objects together), twisted or bent. For example, an arrow gets the elastic potential energy from the bow. When it leaves the bow, the potential energy turns into kinetic energy. The equation of the elastic potential energy is:
- [math]\displaystyle{ U=\frac{1}{2}kx^2 }[/math]
- Which means:
- U is the elastic potential energy.
- k is the spring constant.
- x is the distance pushed or pulled.
Hooke's Law Media
Hooke's law: the force is proportional to the extension
Bourdon tubes are based on Hooke's law. The force created by gas pressure inside the coiled metal tube above unwinds it by an amount proportional to the pressure.
The balance wheel at the core of many mechanical clocks and watches depends on Hooke's law. Since the torque generated by the coiled spring is proportional to the angle turned by the wheel, its oscillations have a nearly constant period.
A mass suspended by a spring is the classical example of a harmonic oscillator
