Euler's identity

Euler's identity, sometimes called Euler's equation, is this equation:

[math]\displaystyle{ e^{i\pi} + 1 = 0 }[/math]

It features the following mathematical constants:

• [math]\displaystyle{ \pi }[/math], pi

  [math]\displaystyle{ \pi \approx 3.14159 }[/math]

• [math]\displaystyle{ e }[/math], Euler's Number

  [math]\displaystyle{ e \approx 2.71828 }[/math]

• [math]\displaystyle{ i }[/math], imaginary unit

  [math]\displaystyle{ i = \sqrt{-1} }[/math]

It also features three of the basic mathematical operations: addition, multiplication and exponentiation.

Euler's identity is named after the Swiss mathematician Leonard Euler. It is not clear that he invented it himself.

Respondents to a Physics World poll called the identity "the most profound mathematical statement ever written", "uncanny and sublime", "filled with cosmic beauty" and "mind-blowing".

Mathematical proof of Euler's Identity using Taylor Series

Many equations can be written as a series of terms added together. This is called a Taylor series.

The exponential function [math]\displaystyle{ e ^{x} }[/math] can be written as the Taylor series

[math]\displaystyle{ e ^{x} = 1 + x + {x^{2}\over{2!}} + {x^{3}\over{3!}} + {x^{4}\over{4!}} \cdots = \sum_{k=0}^\infty {x^{n}\over n!} }[/math]

As well, the sine function can be written as

[math]\displaystyle{ \sin{x} = x - {x^{3} \over 3!} + {x^5 \over 5!} - {x^{7} \over 7!} \cdots = \sum_{k=0}^\infty {(-1)^{n}\over (2n+1)!} {x^{2n+1}} }[/math]

and cosine as

[math]\displaystyle{ \cos{x} = 1 - {x^{2} \over 2!} + {x^4 \over 4!} - {x^{6} \over 6!} \cdots = \sum_{k=0}^\infty {(-1)^{n}\over (2n)!} {x^{2n}} }[/math]

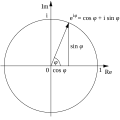
Here, we see a pattern take form. [math]\displaystyle{ e^{x} }[/math] seems to be a sum of sine and cosine's Taylor series, except with all of the signs changed to positive. The identity we are actually proving is [math]\displaystyle{ e^{ix} = \cos(x) + i \sin(x) }[/math].

So, on the left side is [math]\displaystyle{ e^{ix} }[/math], whose Taylor series is [math]\displaystyle{ 1 + ix - {x^{2} \over 2!} - {ix^{3} \over 3!} + {x^{4} \over 4!} + {ix^{5} \over 5!} \cdots }[/math]

We can see a pattern here, that every second term is i times sine's terms, and that the other terms are cosine's terms.

On the right side is [math]\displaystyle{ \cos(x) + i \sin(x) }[/math], whose Taylor series is the Taylor series of cosine, plus i times the Taylor series of sine, which can be shown as:

[math]\displaystyle{ ( 1 - {x^{2} \over 2!} + {x^{4} \over 4!} \cdots) + (ix - {ix^{3} \over 3!} + {ix^{5} \over 5!}\cdots) }[/math]

if we add these together, we have

[math]\displaystyle{ 1 + ix - {x^{2} \over 2!} - {ix^{3} \over 3!} + {x^{4} \over 4!} + {ix^{5} \over 5!} \cdots }[/math]

Therefore,

[math]\displaystyle{ e^{ix} = \cos(x) + i \sin(x) }[/math]

Now, if we replace x with [math]\displaystyle{ \pi }[/math], we have:

[math]\displaystyle{ e^{i\pi} = \cos(\pi) + i \sin(\pi) }[/math]

Since we know that [math]\displaystyle{ \cos(\pi) = -1 }[/math] and [math]\displaystyle{ \sin(\pi) = 0 }[/math], we have:

• [math]\displaystyle{ e^{i\pi} = -1 }[/math]
• [math]\displaystyle{ e^{i\pi} + 1 = 0 }[/math]

which is the statement of Euler's identity.

Euler's Identity Media

• 

  Euler's formula for a general angle

Related pages

• −1 (number)
• Euler's formula