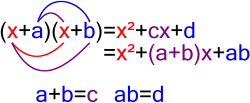Factorization
Factorization (also called factorisation and factoring) is taking a composite number apart into numbers that multiply together to get the original number. These smaller numbers are called factors or divisors. 1 is a factor of all numbers.
Prime factorization is breaking apart a composite number into prime numbers that can be multiplied to give the larger number. Note that since 1 is not prime, it is not included in the prime factorization.
For example, 12 can be factored as 4 × 3. Since 4 is not a prime number, that is not its prime factorization. 12's prime factorization is in fact 3 × 2 × 2.
The numbers which are obtained from the factorization are usually ordered, for example, starting with the smallest number. For example, 72=2^3*3^2. The factorization of every number is unique. This generalizes to:
- Every number has a unique prime factorization
- Every prime factorization corresponds to a unique number
Since finding the numbers to multiply together is very difficult for large numbers, this fact can be used in cryptography.
Polynomials
This is how one type of polynomial is factored.
[math]\displaystyle{ x^2+{\color{Green}9x}+20 }[/math]
Find two numbers that add up to 9 and can be multiplied to get 20. Here, these numbers are 4 and 5.
[math]\displaystyle{ =x^2+{\color{Green}4x+5x}+20 }[/math]
[math]\displaystyle{ =(x^2+4x)+(5x+20) }[/math]
[math]\displaystyle{ =x(x+4)+5(x+4) }[/math]
[math]\displaystyle{ =(x+5)(x+4) }[/math]