File:Regression pic assymetrique.gif
Regression_pic_assymetrique.gif (610 × 460 pixels, file size: 22 KB, MIME type: image/gif, looped, 10 frames, 5.0 s)
| This is a file from the Wikimedia Commons. The description on its description page there is shown below.
|
Summary
| DescriptionRegression pic assymetrique.gif |
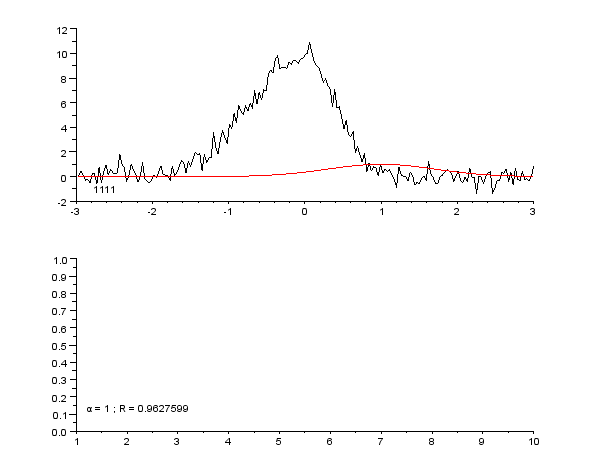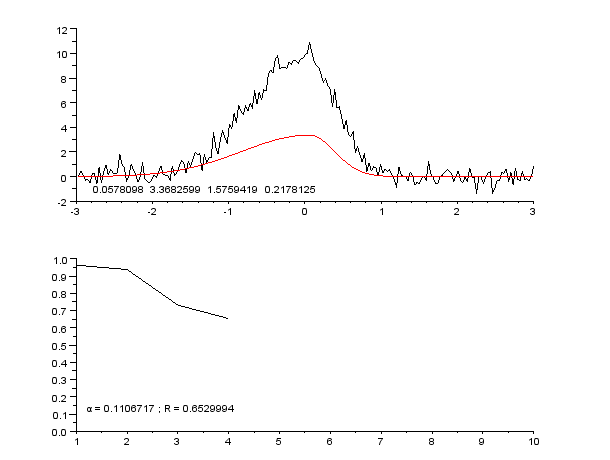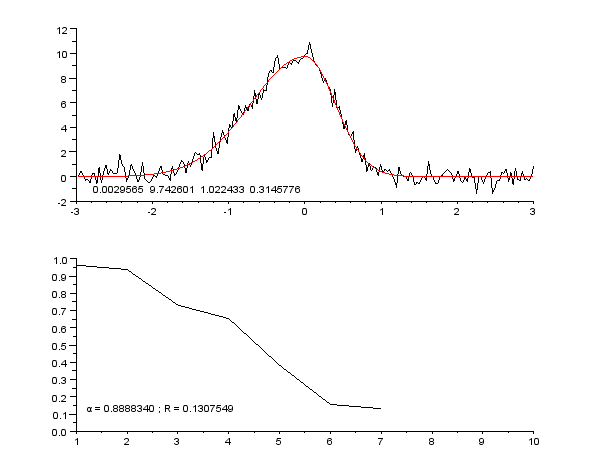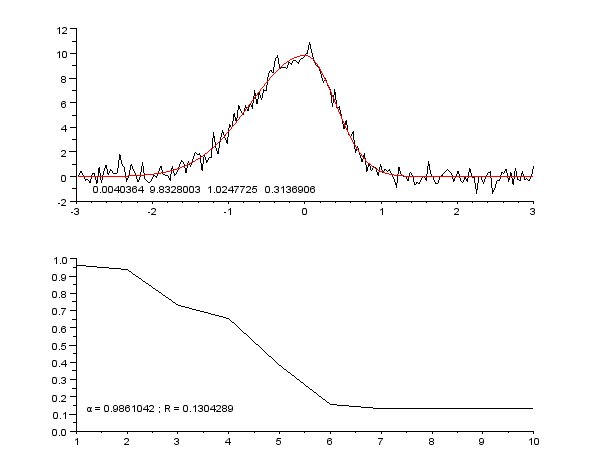
English: Successive steps of Gauss-Newton regression, with variable damping factor α, to fit a dissymetrical noisy peak.
Pictures created with Scilab, animated with The Gimp.
Français : Étapes successives d'une régression de Gauss-Newton, avec facteur d'amortissement α variable, pour ajuster un pic assymétrique.
Images créées avec Scilab ; animation créée avec The Gimp. |
| Date | |
| Source | Own work |
| Author | Cdang (Christophe Dang Ngoc Chan) |
Scilab source
| This media was created with Scilab, a free open-source software. Here is a listing of the Scilab source used to create this file. |
Le fichier de données et celui de fonctions communes sont identiques à ceux de File:Regression pic gaussien dissymetrique bruite.svg.
// **********
// Constantes et initialisation
// **********
clear;
clf;
chdir('monchemin/')
// Paramètres de Newton-Raphson
precision = 1e-7; // condition d'arrêt
itermax = 60; // idem
// Précision de la linéarisation approchée
epsilon = 1e-6;
// **********
// Fonctions
// **********
exec('fonctions_communes.sce', -1)
function [e] = res(Yexp, Ycal)
e = sqrt(sum((Yexp-Ycal).^2));
endfunction
function [A, R] = gaussnewton(f, X, Yexp, A0, imax, epsilon)
// A : jeu de paramètres optimisé par régression (vecteur)
// R : liste des facteurs de qualité de la régression
// pour chaque étape (vecteur)
// X : variable explicative (vecteur)
// Yexp : variable expliquée, valeurs mesurées (vecteur)
// A0 : paramètres d'initialisation du modèle (vecteur)
// epsilon : valeur d'arrêt (scalaire)
k = 1; // facteur d'amortissement initial, <=1,
// évite la divergence
n = size(X,'*');
e0 = sqrt(sum(Yexp.^2)); // normalisation du facteur de qualité
Ycal = f(A0, X); // modèle initial
R(1) = res(Yexp, Ycal)/e0; // facteur de qualité initial
disp('i = 1 ; k = 1 ; R = '+string(R(1))) // affichage param initiaux
i = 1;
B = A0;
subplot(2,1,1)
plot2d(X, Yexp, rect=[-3, -2, 3, 12])
plot(X, Ycal, "-r")
xstring(-2.8, -1.5, string(B))
subplot(2,1,2)
plot2d(R, rect=[1, 0, 10, 1])
xstring(1.2, 0.1, 'α = '+string(k)+' ; R = '+string(R(i)))
nom = 'picassym'+string(i)+'.gif';
xs2gif(0,nom)
drapeau = %t;
while (i < imax) & drapeau // teste la convergence globale
i = i+1;
deltay = Yexp - Ycal;
J = linearisation_approchee(f, B, X, epsilon); // matrice jacobienne
tJ = J'; // transposée
deltap0 = inv((tJ*J))*tJ*deltay;
drapeau2 = %t // pour une 1re exécution
while drapeau2 & (k>0.1) // teste la divergence sur 1 étape
deltap = k*deltap0;
Bnouveau = B + deltap';
Ycal = f(Bnouveau, X);
R(i) = res(Yexp, Ycal)/e0;
drapeau2 = (R(i) >= R(i-1)) // vrai si diverge
if drapeau2 then k = k*0.75; // atténue si diverge
else k0 = k; // pour affichage de la valeur
k = (1 + k)/2; // réduit l'atténuation si converge
end
end
B = Bnouveau;
drapeau = abs(R(i-1) - R(i)) > epsilon
clf;
subplot(2,1,1)
plot2d(X, Yexp, rect=[-3, -2, 3, 12])
plot(X, Ycal, "-r")
xstring(-2.8, -1.5, string(B))
subplot(2,1,2)
plot2d(R, rect=[1, 0, 10, 1])
xstring(1.2, 0.1, 'α = '+string(k0)+' ; R = '+string(R(i)))
nom = 'picassym'+string(i)+'.gif';
xs2gif(0,nom)
// disp('i = '+string(i)+' ; k = '+string(k0)+' ; R = '+string(R(i)))
end
A = B;
endfunction
// **********
// Programme principal
// **********
// lecture des données
donnees = read('pic_gauss_dissym_bruite.txt',-1,2);
// carcatéristiques des données
Xdef = donnees(:,1);
Ydef = donnees(:,2);
// Ainit = [-0.03, 9.7, 8*((0.84 - 0.03)/2.35)^2, 8*((0.45 + 0.03)/2.35)^2];
Ainit = [1, 1, 1, 1];
// Régression
tic();
[Aopt, Rnr] =...
gaussnewton(gauss_dissym, Xdef, Ydef,...
Ainit, itermax, precision)
t = toc();
// Courbe calculée
Yopt = gauss_dissym(Aopt, Xdef);
// Affichage
print(%io(2),Ainit)
print(%io(2),Aopt)
print(%io(2),t)
clf
subplot(2,1,1)
plot(Xdef, Ydef, "-b")
plot(Xdef, Yopt, "-r")
subplot(2,1,2)
plot(Rnr)
Licensing
I, the copyright holder of this work, hereby publish it under the following licenses:

|
Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled GNU Free Documentation License.http://www.gnu.org/copyleft/fdl.htmlGFDLGNU Free Documentation Licensetruetrue |
This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported, 2.5 Generic, 2.0 Generic and 1.0 Generic license.
- You are free:
- to share – to copy, distribute and transmit the work
- to remix – to adapt the work
- Under the following conditions:
- attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.
You may select the license of your choice.
Captions
Add a one-line explanation of what this file represents
Items portrayed in this file
depicts
5 December 2012
image/gif
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Dimensions | User | Comment | |
|---|---|---|---|---|
| current | 05:13, 5 December 2012 | 610 × 460 (22 KB) | Cdang | {{Information |Description ={{en|1=alpha (damping factor) value corrected}} |Source ={{own}} |Author =Cdang |Date = |Permission = |other_versions = }} |
File usage
The following page uses this file:
Metadata
This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.
If the file has been modified from its original state, some details may not fully reflect the modified file.
| GIF file comment | Created with GIMP |
|---|