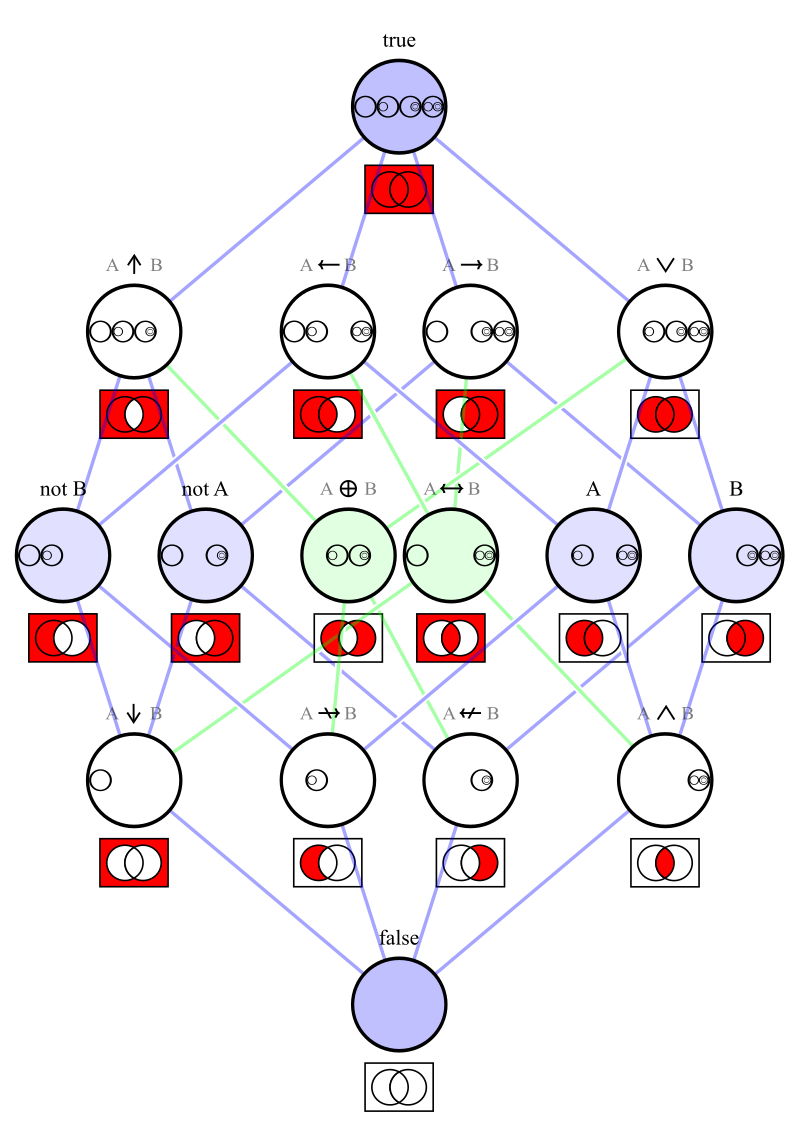
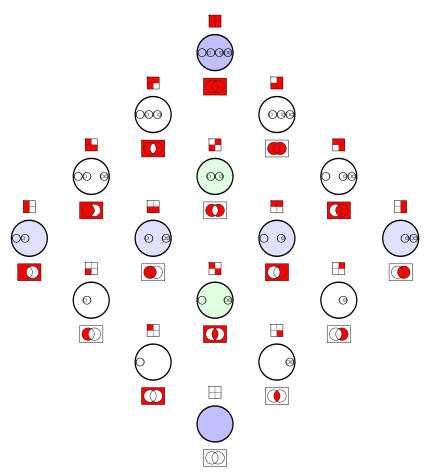
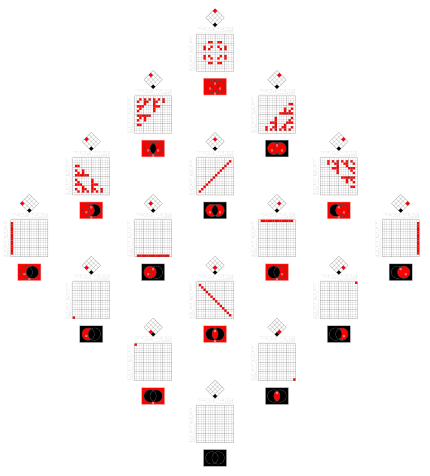
|
|
|
∅c |
|
|
|
|
|
|
|
A = A |
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
 |
|
|
|
|
|
Ac  Bc Bc |
true
A ↔ A |
A  B B |
|
|
|
|
|
A  Bc Bc |
A A A
|
A  Bc Bc |
|
|
|
|
 |
|
 |
|
|
|
|
|
 |
|
 |
|
|
|
A  Bc Bc |
¬A  ¬B ¬B
A → ¬B |
A  B B |
A  B B
A ← ¬B |
Ac  B B |
|
|
|
A  B B |
A ¬B ¬B
|
A = Bc |
A ¬B ¬B
|
A  B B |
|
|
 |
|
 |
|
 |
|
|
|
 |
|
 |
|
 |
|
Bc |
A  ¬B ¬B
A ← B |
A |
A  B B
A ↔ ¬B |
Ac |
¬A  B B
A → B |
B |
|
B = ∅ |
A B B
|
A = ∅c |
A ¬B ¬B
|
A = ∅ |
A B B
|
B = ∅c
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|

|
¬B
|
A  Bc Bc |
A
|
(A  B)c B)c |
¬A
|
Ac  B B |
B
|
|
B false false
|
|
A true true
|
A = B |
A false false
|
|
B true true
|
|
 |
|
 |
|
 |
|
|
|
 |
|
 |
|
 |
|
|
A  ¬B ¬B
|
Ac  Bc Bc |
A  B B
|
A  B B |
¬A  B B
|
|
|
|
|
|
A B B
|
|
|
|
|
|
 |
|
 |
|
|
|
|
|
 |
|
 |
|
|
|
|
¬A  ¬B ¬B
|
∅ |
A  B B
|
|
|
|
|
|
|
A = Ac |
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
false
A ↔ ¬A |
|
|
|
|
|
|
|
A ¬A ¬A
|
|
|
|
These sets (statements) have complements (negations).
They are in the opposite position within this matrix.
|
|
These relations are statements, and have negations.
They are shown in a separate matrix in the box below.
|