Fundamental group

A fundamental group is a concept in algebraic topology. A fundamental group is a group of equivalence classes (a set with things that are the same) of loops in an area. This means that the group gives information about loops in an area. The fundamental group is the simplest type of homotopy group. The fundamental group is also an "homotopy invariant". The fundamental group of a topological space [math]\displaystyle{ X }[/math] is written as an [math]\displaystyle{ \pi_1(X) }[/math].

Intuition

Think of a space. For example, one could start with a surface. In that space, there is a point in that space. All loops in this space start and end at this point. A line can start at this point. The line will then move around and goes back to the starting point. Also, two different loops can be combined. Two loops are thought to be the same if they can be combined into each other without breaking. The set all loops that can be combined and be equal is called the fundamental group.

Fundamental Group Media

• 

  Illustration of en:Double torus

• 

  Homotopy_of_pointed_circle_maps

• 

  Homotopy group addition

• 

  A star domain is simply connected since any loop can be contracted to the center of the domain, denoted x_0.

• 

  A loop on a 2-sphere (the surface of a ball) being contracted to a point

• 

  Fundamental_group_of_the_circle

• 

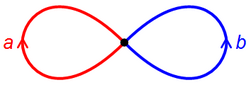
  The fundamental group of the figure eight is the free group on two generators a and b.

• 

  This is the mirror image of TrefoilKnot-01.png: 

• 

  The map \mathbb{R} \times [0,1] \to S^1 \times [0,1] is a covering: the preimage of U (highlighted in gray) is a disjoint union of copies of U. Moreover, it is a universal covering since \mathbb{R} \times [0,1] is contractible and therefore simply connected.

References

• Adams, John Frank (1978), Infinite loop spaces, Annals of Mathematics Studies, vol. 90, Princeton University Press, ISBN 978-0-691-08207-3, MR 0505692
• Brown, Ronald (2006), Topology and Groupoids, Booksurge, ISBN 1-4196-2722-8
• Bump, Daniel (2013), Lie Groups, Graduate Texts in Mathematics, vol. 225 (2nd ed.), Springer, doi:10.1007/978-1-4614-8024-2, ISBN 978-1-4614-8023-5
• Crowell, Richard H.; Fox, Ralph (1963), Introduction to Knot Theory, Springer
• El Zein, Fouad; Suciu, Alexander I.; Tosun, Meral; Uludağ, Muhammed; Yuzvinsky, Sergey (2010), Arrangements, Local Systems and Singularities: CIMPA Summer School, Galatasaray University, Istanbul, 2007, ISBN 978-3-0346-0208-2
• Forster, Otto (1981), Lectures on Riemann Surfaces, ISBN 0-387-90617-7
• Fulton, William (1995), Algebraic Topology: A First Course, Springer, ISBN 9780387943275
• Goerss, Paul G.; Jardine, John F. (1999), Simplicial Homotopy Theory, Progress in Mathematics, vol. 174, Basel, Boston, Berlin: Birkhäuser, ISBN 978-3-7643-6064-1
• Grothendieck, Alexandre; Raynaud, Michèle (2003) [1971], Séminaire de Géométrie Algébrique du Bois Marie - 1960-61 - Revêtements étales et groupe fondamental - (SGA 1) (Documents Mathématiques 3), Paris: Société Mathématique de France, pp. xviii+327, see Exp. V, IX, X, arXiv:math.AG/0206203, ISBN 978-2-85629-141-2
• Hall, Brian C. (2015), Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, Graduate Texts in Mathematics, vol. 222 (2nd ed.), Springer, ISBN 978-3319134666
• Hatcher, Allen (2002), Algebraic Topology, Cambridge University Press, ISBN 0-521-79540-0
• Peter Hilton and Shaun Wylie, Homology Theory, Cambridge University Press (1967) [warning: these authors use contrahomology for cohomology]
• Humphreys, James E. (2004), Linear Algebraic Groups, Graduate Texts in Mathematics, Springer, ISBN 9780387901084
• Humphreys, James E. (1972), Introduction to Lie Algebras and Representation Theory, ISBN 0-387-90052-7
• Maunder, C. R. F. (January 1996), Algebraic Topology, Dover Publications, ISBN 0-486-69131-4
• Massey, William S. (1991), A Basic Course in Algebraic Topology, Springer, ISBN 038797430X
• May, J. Peter (1999), A Concise Course in Algebraic Topology, ISBN 9780226511832
• Deane Montgomery and Leo Zippin, Topological Transformation Groups, Interscience Publishers (1955)
• Munkres, James R. (2000), Topology, Prentice Hall, ISBN 0-13-181629-2
• Rotman, Joseph (1998-07-22), An Introduction to Algebraic Topology, Springer-Verlag, ISBN 0-387-96678-1
• Rubei, Elena (2014), Algebraic Geometry, a concise dictionary, Berlin/Boston: Walter De Gruyter, ISBN 978-3-11-031622-3
• Seifert, Herbert; Threlfall, William (1980), A Textbook of Topology, translated by Heil, Wolfgang, Academic Press, ISBN 0-12-634850-2
• Singer, Isadore. M.; Thorpe, J. A. (1976-12-10), Lecture Notes on Elementary Topology and Geometry, ISBN 0-387-90202-3
• Spanier, Edwin H. (1989), Algebraic Topology, Springer, ISBN 0-387-94426-5
• Strom, Jeffrey (2011), Modern Classical Homotopy Theory, AMS, ISBN 9780821852866

Other websites

• Weisstein, Eric W., "Fundamental group" from MathWorld.
• Dylan G.L. Allegretti, Simplicial Sets and van Kampen's Theorem: A discussion of the fundamental groupoid of a topological space and the fundamental groupoid of a simplicial set
• Animations to introduce fundamental group by Nicolas Delanoue
• Sets of base points and fundamental groupoids: mathoverflow discussion
• Groupoids in Mathematics