Hexahedron

A hexahedron (plural: hexahedra) is any polyhedron with six faces. A cube, for example, is a regular hexahedron with all its faces square, and three squares around each vertex.

There are seven topologically distinct convex hexahedra, one of which exists in two mirror image forms. (Two polyhedra are "topologically distinct" if they have intrinsically different arrangements of faces and vertices, such that it is impossible to distort one into the other simply by changing the lengths of edges or the angles between edges or faces.)

Quadrilaterally-faced hexahedron (Cuboid) 6 faces, 12 edges, 8 vertices
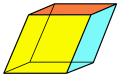
Cube (square)	Rectangular cuboid (three pairs of rectangles)	Trigonal trapezohedron (congruent rhombi)	Trigonal trapezohedron (congruent quadrilaterals)	Quadrilateral frustum (apex-truncated square pyramid)	Parallelepiped (three pairs of parallelograms)	(three pairs of rhombi)
Oh, [4,3], (*432) order 48	D2h, [2,2], (*222) order 8	D3d, [2+,6], (2*3) order 12	D3, [2,3]+, (223) order 6	C4v, [4], (*44) order 8	Ci, [2+,2+], (×) order 2

Others

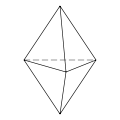Triangular bipyramid 36 Faces 9 E, 5 V

Tetragonal antiwedge. Chiral – exists in "left-handed" and "right-handed" mirror image forms. 4.4.3.3.3.3 Faces 10 E, 6 V

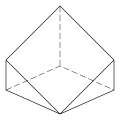4.4.4.4.3.3 Faces 11 E, 7 V

Pentagonal pyramid 5.35 Faces 10 E, 6 V

5.4.4.3.3.3 Faces 11 E, 7 V

5.5.4.4.3.3 Faces 12 E, 8 V

There are three further topologically distinct hexahedra that can only be realised as concave figures:

Concave
4.4.3.3.3.3 Faces 10 E, 6 V	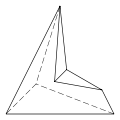5.5.3.3.3.3 Faces 11 E, 7 V	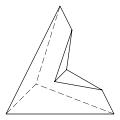6.6.3.3.3.3 Faces 12 E, 8 V

Hexahedron Media

• 
• Cuboid.png的無文字版本

Related pages

• Prismatoid

Other websites

• Polyhedra with 4-7 Faces Archived 2006-09-04 at the Wayback Machine by Steven Dutch