Irrational number
In mathematics, an irrational number is a real number that cannot be written as a complete ratio of two integers.
An irrational number cannot be fully written down in fraction or decimal form. It would have an infinite number of digits. In addition, these digits would also not repeat. The set of irrational numbers is sometimes written as [math]\displaystyle{ \mathbb{R}-\mathbb{Q} }[/math] or [math]\displaystyle{ \overline{\mathbb{Q}} }[/math]. [1][2][3]
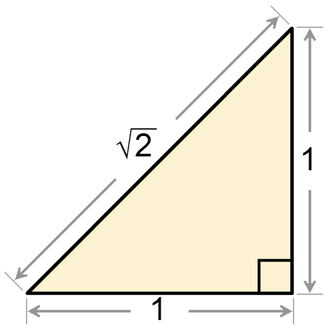
Irrational numbers often occur in geometry. For instance, if a square has sides of 1 meter, the distance between opposite corners is the square root of two meters. This is an irrational number. In decimal form it is written as 1.414213... Mathematicians have proved that the square root of every natural number is either an integer or an irrational number.
One well known irrational number is pi (π). This is the circumference of a circle divided by its diameter. This number is the same for every circle. The number pi is approximately 3.14159265358979323… .
Other examples of irrational number include the numbers [math]\displaystyle{ e }[/math] and [math]\displaystyle{ \sqrt{3} }[/math]. A number for which irrationality is not known is the Euler–Mascheroni constant [math]\displaystyle{ \gamma }[/math].[2]
Irrational Number Media
The number \sqrt{2} is irrational.
An Euler diagram showing the set of real numbers (\mathbb {R}), which include the rationals (\mathbb {Q}), which include the integers (\mathbb {Z}), which include the natural numbers (\mathbb {N}). The real numbers also include the irrationals (\mathbb {R}\\mathbb {Q}).
Related pages
References
- ↑ "Comprehensive List of Algebra Symbols". Math Vault. 2020-03-25. Retrieved 2020-10-12.
- ↑ 2.0 2.1 Weisstein, Eric W. "Irrational Number". mathworld.wolfram.com. Retrieved 2020-10-12.
- ↑ "Irrational Numbers". www.learnalberta.ca. Retrieved 2020-10-12.