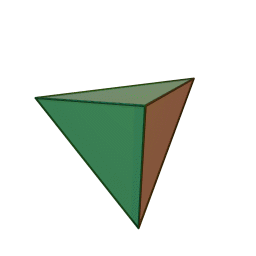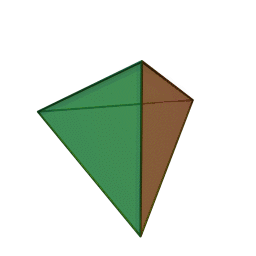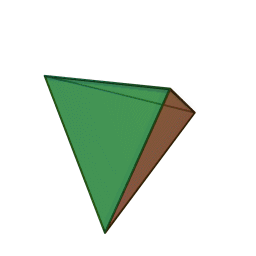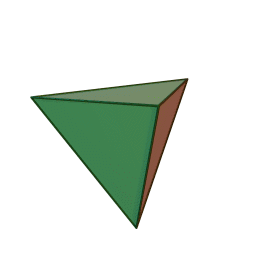
Tetrahedron
A tetrahedron or triangular pyramid is a polyhedron (a three-dimensional shape). It has four corners and six edges. All four of its faces are equilateral triangles. Every two edges meet on one of those corners forming a sixty-degree angle.
Formulas for a regular tetrahedron
A regular tetrahedron is a tetrahedron whose edges are the same length. If the length of an edge is a:
| Surface area[1] | [math]\displaystyle{ {\sqrt{3}}a^2\, }[/math] |
| Face area | [math]\displaystyle{ \frac{\sqrt{3}}{4}a^2\, }[/math] |
| Height[2] | [math]\displaystyle{ \sqrt{\frac23}\,a\, }[/math] and [math]\displaystyle{ \frac{\sqrt{6}}{3}a }[/math] |
| Volume[1] | [math]\displaystyle{ \frac{a^3}{6\sqrt{2}}\, }[/math] and [math]\displaystyle{ \frac{\sqrt{2}}{12}a^3 }[/math] |
Other properties
A regular tetrahedron's faces are all the same, and so are all its edges, as well as its corners. This makes it a regular polyhedron. It is also convex (its faces do not go through one another), which makes it a Platonic solid.
The dual of regular tetrahedron is another regular tetrahedron. This is called being self-dual.
Tetrahedron Media
A space-filling tetrahedral disphenoid inside a cube. Two edges have dihedral angles of 90°, and four edges have dihedral angles of 60°.
A cube dissected into six characteristic orthoschemes.
For Euclidean 3-space, there are 3 simple and related Goursat tetrahedra. They can be seen as points on and within a cube.
Six edge-lengths of Tetrahedron
Illustration of the law of sines for tetrahedra
References
- ↑ 1.0 1.1 Coxeter, Harold Scott MacDonald; Regular Polytopes, Methuen and Co., 1948, Table I(i)
- ↑ Köller, Jürgen, "Tetrahedron", Mathematische Basteleien, 2001