Unit circle
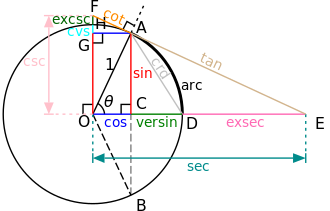
In mathematics, a unit circle is a circle with a radius of 1. The equation of the unit circle is [math]\displaystyle{ x^2 + y^2 = 1 }[/math]. The unit circle is centered at the Origin, or coordinates (0,0). It is often used in Trigonometry.
Trigonometric functions in the unit circle
In a unit circle, where [math]\displaystyle{ t }[/math] is the angle desired, [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] can be defined as [math]\displaystyle{ \cos (t) = x }[/math] and [math]\displaystyle{ \sin (t) = y }[/math]. Using the function of the unit circle, [math]\displaystyle{ x^2 + y^2 = 1 }[/math], another equation for the unit circle is found, [math]\displaystyle{ \cos^2(t) + \sin^2(t) = 1 }[/math]. When working with trigonometric functions, it is mainly useful to use angles with measures between 0 and [math]\displaystyle{ \pi\over 2 }[/math] radians, or 0 through 90 degrees. It is possible to have higher angles than that, however. Using the unit circle, two identities can be found: [math]\displaystyle{ \cos (t) = \cos (2 \cdot \pi k + t) }[/math] and [math]\displaystyle{ sin (t) = \sin (2 \cdot \pi k + t) }[/math] for any integer [math]\displaystyle{ k }[/math].
