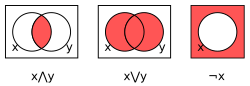
Boolean algebra
In mathematics, Boolean algebra is an algebra for binary digits (where 0 means false and 1 means true).[1] It is equipped with three operators: conjunction (AND), disjunction (OR) and negation (NOT).[2] It uses normal math symbols, but it does not work in the same way. It is named for George Boole,[3] who invented it in the middle 19th century. Boolean algebra did not get much attention except from mathematicians until the 20th century when engineers began using it for logic gates.
NOT gate
| NOT | |
|---|---|
| 0 | 1 |
| 1 | 0 |
The NOT operator is written with a bar over numbers or letters like this:
- [math]\displaystyle{ \bar{1} = 0 }[/math]
- [math]\displaystyle{ \bar{0} = 1 }[/math]
- [math]\displaystyle{ \bar{\mbox{A}} = \mbox{Q} }[/math]
It means that the output is not the input.
AND gate
| AND | 0 | 1 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
The AND operator is written as [math]\displaystyle{ \cdot }[/math] like this:[5]
- [math]\displaystyle{ 0 \cdot 0 = 0 }[/math]
- [math]\displaystyle{ 0 \cdot 1 = 0 }[/math]
- [math]\displaystyle{ 1 \cdot 0 = 0 }[/math]
- [math]\displaystyle{ 1 \cdot 1 = 1 }[/math]
The output is true if and only if one and the other input is true.
OR gate
| OR | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 1 |
The OR operator is written as [math]\displaystyle{ + }[/math] like this:[5]
- [math]\displaystyle{ 0 + 0 = 0 }[/math]
- [math]\displaystyle{ 0 + 1 = 1 }[/math]
- [math]\displaystyle{ 1 + 0 = 1 }[/math]
- [math]\displaystyle{ 1 + 1 = 1 }[/math]
If one or the other input is true, then the output to be true (and false otherwise).
XOR gate
| XOR | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
XOR basically means "exclusive or", meaning one input or the other must be true, but not both. It is also sometimes called NOR, which means the same thing.
The XOR operator is written as [math]\displaystyle{ - }[/math] like this:
- [math]\displaystyle{ 0 - 0 = 0 }[/math]
- [math]\displaystyle{ 0 - 1 = 1 }[/math]
- [math]\displaystyle{ 1 - 0 = 1 }[/math]
- [math]\displaystyle{ 1 - 1 = 0 }[/math]
In other words, the XOR operator returns true precisely when one or the other input is true—but not both.
Identities
Different gates can be put together in different orders:
- [math]\displaystyle{ \overline{\mbox{A} \cdot \mbox{B}} }[/math] is the same as an AND then a NOT. This is called a NAND gate.
It is not the same as a NOT then an AND: [math]\displaystyle{ \overline{\mbox{A}} \cdot \overline{\mbox{B}} }[/math]
- [math]\displaystyle{ \mbox{A} + 1 = 1 }[/math]
- [math]\displaystyle{ \mbox{A} \cdot 1 = \mbox{A} }[/math]
which is called AND identity table
| AND | 1 | 0 | Any |
|---|---|---|---|
| 1 | TRUE | 0 | 0 |
| 0 | 0 | 0 | [math]\displaystyle{ \overline{ANY} }[/math] |
| Any | 0 | [math]\displaystyle{ \overline{ANY} }[/math] | [math]\displaystyle{ \{Any\} }[/math] |
, if [math]\displaystyle{ ANY=\{x|\{x\}=\{\{TRUE\}\or\{\overline{TRUE}\}, \};\and (TRUE, 0) \vdash TRUE \and \overline{0} = \{x\} }[/math].[source?]
or if [math]\displaystyle{
ANY=\{x \|\{TRUE\}, \{\overline{TRUE}\} .\}, }[/math]=TRUE, TRUE.,
De Morgan's laws
Augustus De Morgan discovered that it is possible to preserve the truth values of Boolean expressions by changing a [math]\displaystyle{ + }[/math] sign to a [math]\displaystyle{ \cdot }[/math] sign, while making or breaking a bar. That is:
- [math]\displaystyle{ \overline{\mbox{A} + \mbox{B}} = \overline{\mbox {A}} \cdot \overline{\mbox{B}} }[/math]
- [math]\displaystyle{ \overline{\mbox{A} \cdot \mbox{B}} = \overline{\mbox {A}} + \overline{\mbox{B}} }[/math]
These findings are commonly known as De Morgan's laws.
Boolean Algebra Media
Figure 2. Venn diagrams for conjunction, disjunction, and complement
Schematic symbols for the De Morgan duals of AND and OR gates and inverters
Related pages
References
- ↑ "Comprehensive List of Logic Symbols". Math Vault. 2020-04-06. Retrieved 2020-09-02.
- ↑ Weisstein, Eric W. "Boolean Algebra". mathworld.wolfram.com. Retrieved 2020-09-02.
- ↑ "Boolean algebra | Define Boolean algebra at Dictionary.com". Dictionary.reference.com. 1997-02-27. Retrieved 2010-08-12.
- ↑ 4.0 4.1 4.2 4.3 "Logic Gates". Kpsec.freeuk.com. Retrieved 2010-08-12.
- ↑ 5.0 5.1 "Elements of Boolean Algebra". www.ee.surrey.ac.uk. Archived from the original on 2020-07-21. Retrieved 2020-09-02.
Other websites
- Boolean algebra on All About Circuits
- Boolean algebra Citizendium