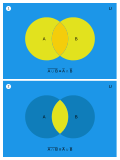
De Morgan's laws
In boolean algebra, DeMorgan's laws are the laws of how a NOT gate affects AND and OR statements:[1]
- [math]\displaystyle{ \overline{A \cdot B} = \overline {A} + \overline {B} }[/math]
- [math]\displaystyle{ \overline{A + B} = \overline {A} \cdot \overline {B} }[/math]
They can be remembered by "break the line, change the sign".
Truth tables
The following truth tables prove DeMorgan's laws.
| INPUT | OUTPUT 1 | OUTPUT 2 | |
| A | B | NOT (A AND B) | (NOT A) OR (NOT B) |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| INPUT | OUTPUT 1 | OUTPUT 2 | |
| A | B | NOT (A OR B) | (NOT A) AND (NOT B) |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 |
De Morgan's Laws Media
De Morgan's laws represented with Venn diagrams. In each case, the resultant set is the set of all points in any shade of blue.
The equivalency of ¬φ ∨ ¬ψ and ¬(φ ∧ ψ) is displayed in this truth table.
De Morgan's law with set subtraction operation.
De Morgan's Laws represented as a circuit with logic gates (International Electrotechnical Commission diagrams).
