Factorial

The factorial of a whole number [math]\displaystyle{ n }[/math], written as [math]\displaystyle{ n! }[/math] or [math]\displaystyle{ n }[/math], is found by multiplying [math]\displaystyle{ n }[/math] by all the whole numbers less than it. For example, the factorial of 4 is 24, because [math]\displaystyle{ 4 \times 3 \times 2 \times 1 = 24 }[/math]. Hence one can write [math]\displaystyle{ 4! = 24 }[/math]. For some technical reasons, 0! is equal to 1.

Factorials can be used to find out how many possible ways there are to arrange [math]\displaystyle{ n }[/math] objects.

For example, if there are 3 letters (A, B, and C), they can be arranged as ABC, ACB, BAC, BCA, CAB, and CBA. That is be 6 choices because A can be put in 3 different places, B has 2 choices left after A is placed, and C has only one choice left after A and B are placed. In other words, [math]\displaystyle{ 3 \times 2 \times 1 = 6 }[/math] choices.

The factorial function is a good example of recursion (doing things over and over), as [math]\displaystyle{ 3! }[/math] can be written as [math]\displaystyle{ 3 \times 2! }[/math], which can be written as [math]\displaystyle{ 3 \times 2 \times 1! }[/math] and finally as [math]\displaystyle{ 3 \times 2 \times 1 \times 0! }[/math]. Because of this, [math]\displaystyle{ n! }[/math] can also be defined as [math]\displaystyle{ n \times (n-1)! }[/math], with [math]\displaystyle{ 0! = 1 }[/math]

The factorial function grows very fast. There are [math]\displaystyle{ 10! = 3,628,800 }[/math] ways to arrange 10 items.

Applications

The earliest uses of the factorial function involve counting permutations: there are [math]\displaystyle{ n! }[/math] different ways of arranging [math]\displaystyle{ n }[/math] distinct objects into a sequence. Factorials appear more broadly in many formulas in combinatorics, to account for different orderings of objects. For instance the binomial coefficients [math]\displaystyle{ \tbinom{n}{k} }[/math] count the [math]\displaystyle{ k }[/math]-element combinations (subsets of [math]\displaystyle{ k }[/math] elements) from a set with [math]\displaystyle{ n }[/math] elements, and can be computed from factorials using the formula

[math]\displaystyle{ \binom{n}{k}=\frac{n!}{k!(n-k)!}. }[/math]Related sequences and functions

Main page: List of factorial and binomial topics

Several other integer sequences are similar to or related to the factorials:

Alternating factorial

The alternating factorial is the absolute value of the alternating sum of the first [math]\displaystyle{ n }[/math] factorials, [math]\displaystyle{ \sum_{i = 1}^n (-1)^{n - i}i! }[/math]. These have mainly been studied in connection with their primality; only finitely many of them can be prime, but a complete list of primes of this form is not known.

Factorial Media

• 

  Comparison of the factorial, Stirling's approximation, and the simpler approximation (n/e)^n, on a doubly logarithmic scale

• 

  Relative error in a truncated Stirling series vs. number of terms

• 

  The gamma function (shifted one unit left to match the factorials) continuously interpolates the factorial to non-integer values

• 

  Absolute values of the complex gamma function, showing poles at non-positive integers

• 

  TI SR-50A, a 1975 calculator with a factorial key (third row, center right)

Notes

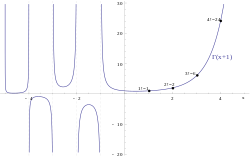
Factorials are not defined for negative numbers. However, the related gamma function ([math]\displaystyle{ \Gamma(x) }[/math]) is defined over the real and complex numbers (except for negative integers).

Related pages

• Exclamation mark
• Permutation

Other websites

• Calculation of Factorial (0≤N≤40000)