Fermi-Dirac statistics
Fermi-Dirac statistics is a branch of quantum statistics. It is named after Enrico Fermi and Paul Dirac. It is used to describe the macroscopic state of a system which is made of many simliar particles (Fermions). One example is to describe the state of electrons in metals and semimetals, to describe electrical conductivity.
Fermi-Dirac statistics makes the following assumptions:
- None of the states of the particles can hold more than one particle (known as Pauli exclusion principle)
- Exchanging a particle for another similar particle will not lead to a new state, but will give the same state (known as Identical particles)
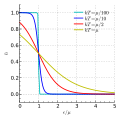
The Fermi distribution tells with what probability, a Fermi gas, at a given temperature and energy level, will have a particle in the given state.
Fermi-Dirac Statistics Media
Equilibrium thermal distributions for particles with integer spin (bosons, red), half integer spin (fermions, blue), and classical (spinless) particles (green). Average occupancy \langle n\rangle is shown versus energy \epsilon relative to the system chemical potential \mu, where T is the system temperature, and k_B is the Boltzmann constant.
Fermi function F(\epsilon) with \mu = 0.55~\text{eV} for various temperatures in the range 2~\text{K} \leq T \leq 375~\text{K}
Energy dependence. More gradual at higher T. \bar{n} = 0.5 when \varepsilon = \mu. Not shown is that \mu decreases for higher T.
Temperature dependence for \varepsilon > \mu.
