Field axioms
References
- ↑
Field Axioms Media
The regular heptagon cannot be constructed using only a straightedge and compass construction; this can be proven using the field of constructible numbers.
The multiplication of complex numbers can be visualized geometrically by rotations and scalings.
- Error creating thumbnail: About to transcode 1 SVG file(s)
Converting Root_construction_geometric_mean5.svg to /var/www/html/w/images/temp/transform_3ec23cb9403a.png ... org.apache.batik.transcoder.TranscoderException: null Enclosed Exception: file:/var/www/html/w/images/temp/svg_1f13017d65d27400a031207e/Root_construction_geometric_mean5.svg:-1 Cannot find the referenced element: "file:/var/www/html/w/images/temp/svg_1f13017d65d27400a031207e/Root_construction_geometric_mean5.svg#clip1" specified on the element <g> - may be a problem of 'id' at org.apache.batik.transcoder.SVGAbstractTranscoder.transcode(SVGAbstractTranscoder.java:228) at org.apache.batik.transcoder.image.ImageTranscoder.transcode(ImageTranscoder.java:92) at org.apache.batik.transcoder.XMLAbstractTranscoder.transcode(XMLAbstractTranscoder.java:142) at org.apache.batik.transcoder.SVGAbstractTranscoder.transcode(SVGAbstractTranscoder.java:158) at org.apache.batik.apps.rasterizer.SVGConverter.transcode(SVGConverter.java:1008) at org.apache.batik.apps.rasterizer.SVGConverter.execute(SVGConverter.java:719) at org.apache.batik.apps.rasterizer.Main.execute(Main.java:956) at org.apache.batik.apps.rasterizer.Main.main(Main.java:1009) Caused by: org.apache.batik.bridge.BridgeException: file:/var/www/html/w/images/temp/svg_1f13017d65d27400a031207e/Root_construction_geometric_mean5.svg:-1 Cannot find the referenced element: "file:/var/www/html/w/images/temp/svg_1f13017d65d27400a031207e/Root_construction_geometric_mean5.svg#clip1" specified on the element <g> - may be a problem of 'id' at org.apache.batik.bridge.BridgeContext.getReferencedNode(BridgeContext.java:762) at org.apache.batik.bridge.BridgeContext.getReferencedElement(BridgeContext.java:804) at org.apache.batik.bridge.CSSUtilities.convertClipPath(CSSUtilities.java:718) at org.apache.batik.bridge.AbstractGraphicsNodeBridge.buildGraphicsNode(AbstractGraphicsNodeBridge.java:146) at org.apache.batik.bridge.GVTBuilder.buildGraphicsNode(GVTBuilder.java:224) at org.apache.batik.bridge.GVTBuilder.buildComposite(GVTBuilder.java:171) at org.apache.batik.bridge.GVTBuilder.buildGraphicsNode(GVTBuilder.java:219) at org.apache.batik.bridge.GVTBuilder.buildComposite(GVTBuilder.java:171) at org.apache.batik.bridge.GVTBuilder.buildGraphicsNode(GVTBuilder.java:219) at org.apache.batik.bridge.GVTBuilder.buildComposite(GVTBuilder.java:171) at org.apache.batik.bridge.GVTBuilder.build(GVTBuilder.java:82) at org.apache.batik.transcoder.SVGAbstractTranscoder.transcode(SVGAbstractTranscoder.java:210) ... 7 more ... error (SVGConverter.error.while.rasterizing.file)
The geometric mean theorem asserts that h2 = pq. Choosing q = 1 allows construction of the square root of a given constructible number p.
In modular arithmetic modulo 12, 9 + 4 = 1 since 9 + 4 = 13 in Z, which divided by 12 leaves remainder 1. However, Z/12Z is not a field because 12 is not a prime number.
Each bounded real set has a least upper bound.
The sum of three points P, Q, and R on an elliptic curve E (red) is zero if there is a line (blue) passing through these points.
A compact Riemann surface of genus two (two handles). The genus can be read off the field of meromorphic functions on the surface.
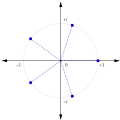
The fifth roots of unity form a regular pentagon.
Weisstein, Eric W.. Field Axioms (in en). mathworld.wolfram.com. Retrieved 2021-09-15.
- ↑ Apostol, T. M. "The Field Axioms." §I 3.2 in Calculus, 2nd ed., Vol. 1: One-Variable Calculus, with an Introduction to Linear Algebra. Waltham, MA: Blaisdell, pp. 17-19, 1967.
