Formal language
In mathematics, computer science and linguistics, a formal language is one that has a particular set of symbols, and whose expressions are made according to a particular set of rules. The symbol [math]\displaystyle{ \mathcal{L} }[/math] is often used as a variable for formal languages in logic.[1]
Unlike natural languages, the symbols and formulas in formal languages are syntactically and semantically related to one another in a precise way.[2] As a result, formal languages are completely (or almost completely) void of ambiguity.[3]
Examples
Some examples of formal languages include:
- The set of all words over [math]\displaystyle{ {a, b}\, }[/math]
- The set [math]\displaystyle{ \left \{ a^{n}\right\} }[/math], where [math]\displaystyle{ n\, }[/math] is a natural number and [math]\displaystyle{ a^n\, }[/math] means [math]\displaystyle{ a\, }[/math] repeated [math]\displaystyle{ n }[/math] times
- Finite languages, such as [math]\displaystyle{ \{\{a,b\},\{a, aa, bba\}\}\, }[/math]
- The set of syntactically correct programs in a given programming language
- The set of inputs upon which a certain Turing machine halts
Specification
A formal language can be specified in a great variety of ways, such as:
- Strings produced by some formal grammar (see Chomsky hierarchy)
- Strings described or matched by a regular expression
- Strings accepted by some automaton, such as a Turing machine or finite state automaton
- Strings indicated by a decision procedure (a set of related yes/no questions) where the answer is 'yes'
Formal Language Media
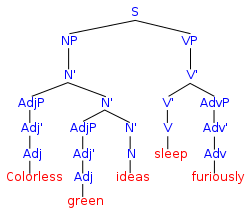
Structure of the syntactically well-formed, although thoroughly nonsensical, English sentence, "Colorless green ideas sleep furiously" (historical example from Chomsky 1957)
This diagram shows the syntactic divisions within a formal system. Strings of symbols may be broadly divided into nonsense and well-formed formulas. The set of well-formed formulas is divided into theorems and non-theorems.
Related pages
- Language for languages in general
- Syntax for the form of a language in general
- Semantics for the meanings in a language
- Natural language for languages that are not formal
- Computer language for application of formal languages in computing
- Programming language for the application of formal languages to program computers
References
- ↑ "Comprehensive List of Logic Symbols". Math Vault. 2020-04-06. Retrieved 2020-10-09.
- ↑ "Definition of formal language | Dictionary.com". www.dictionary.com. Retrieved 2020-10-09.
- ↑ "1.11. Formal and Natural Languages — How to Think like a Computer Scientist: Interactive Edition". runestone.academy. Retrieved 2020-10-09.
Further reading
- Hopcroft, J.; Ullman, J. (1979). Introduction to Automata Theory, Languages, and Computation. Addison-Wesley. ISBN 0-201-02988-X.
- Rasiowa, Helena; Sikorski, Roman (1970). "Chapter 6. Algebra of formalized languages". The Mathematics of Metamathematics (3rd ed.). PWN.
- Rozemberg, G.; Salomaa, A., eds. (1979). Introduction to Automata Theory, Languages, and Computation. Addison-Wesley. ISBN 978-3-540-61486-9.
Other websites
- http://icalp06.dsi.unive.it/ Archived 2006-06-09 at the Wayback Machine ICALP 2006 33rd International Colloquium on Automata, Languages and Programming.
- http://www.cs.auckland.ac.nz/CDMTCS/conferences/dlt/DLTConfSeries.html International Conferences on Developments in Language Theory