Fourier transform

The Fourier transform is a mathematical function that can be used to find the base frequencies that a wave is made of. Imagine playing a chord on a piano. When played, the sounds of the notes of the chord mix together and form a sound wave. This works because each of the different note's waves interfere with each other by adding together or canceling out at different points in the wave. A Fourier transform takes this complex wave and is able to find the frequencies that made it, meaning it can find the notes that a chord is made from.

The output of a Fourier transform is sometimes called a frequency spectrum or distribution because it displays a distribution of possible frequencies of the input. This function has many uses in cryptography, oceanography, machine learning, radiology, quantum physics as well as sound design and visualization.

The Fourier transform of a function [math]\displaystyle{ f(x) }[/math], sometimes written as [math]\displaystyle{ \mathcal{F}\{f\} }[/math], is given by

[math]\displaystyle{ F(\alpha)=\int_{-\infty}^{+\infty} f(x) e^{-2 \pi i \alpha x} \, dx }[/math]

where:

• [math]\displaystyle{ \alpha }[/math] is a frequency.
• [math]\displaystyle{ F(\alpha) }[/math] is the Fourier transform function and returns a value representing how prevalent frequency [math]\displaystyle{ \alpha }[/math] is in the original signal.
• [math]\displaystyle{ e^{-2\pi i \alpha x} }[/math] represents wrapping the input wave function [math]\displaystyle{ f(x) }[/math] around the origin of the complex plane at some frequency [math]\displaystyle{ \alpha }[/math].

The inverse Fourier transform is given by

[math]\displaystyle{ f(x)=\int_{-\infty}^{+\infty} F(\alpha) e^{+2 \pi i x \alpha} \, d \alpha }[/math]

A Fourier transform shows what frequencies are in a signal. For example, consider a sound wave which contains three different musical notes: A, B, and C. Making a graph of the Fourier transform of this sound wave (with the frequency on the x-axis and the intensity on the y-axis) will show a peak at each frequency which corresponds with one of the musical notes.

Many signals can be created by adding cosines and sines together with varying amplitudes and frequencies. The Fourier transform plots the amplitudes and phases of these cosines and sines against their respective frequencies.

Fourier transforms are important, because many signals make more sense when their frequencies are separated. In the audio example above, looking at the signal with respect to time does not make it obvious that the notes A, B, and C are in the signal. Many systems do different things to different frequencies, so these kinds of systems can be described by what they do to each frequency. An example of this is a filter which blocks high frequencies.

Calculating a Fourier transform requires understanding of integration and imaginary numbers. Computers are usually used to calculate Fourier transforms of anything but the simplest signals. The Fast Fourier Transform is a method computers use to quickly calculate a Fourier transform.

• 

  Original function showing a signal oscillating at 3 hertz.

• 

  Real and imaginary parts of integrand for Fourier transform at 3 hertz

• 

  Real and imaginary parts of integrand for Fourier transform at 5 hertz

• 

  Fourier transform with 3 and 5 hertz labeled.

Fourier Transform Media

• 

  An example application of the Fourier transform is determining the constituent pitches in a musical waveform. This image is the result of applying a constant-Q transform (a Fourier-related transform) to the waveform of a C major piano chord.

• 

  Animation showing the Fourier Transform of a time shifted signal. [Top] the original signal (yellow), is continuously time shifted (blue). [Bottom] The resultant Fourier Transform of the time shifted signal. Note how the higher frequency components revolve in complex plane faster than the lower frequency components.

• 

  The rectangular function is Lebesgue integrable.

• 

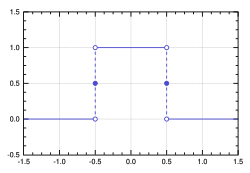
  The sinc function, which is the Fourier transform of the rectangular function, is bounded and continuous, but not Lebesgue integrable.

• 

  Some problems, such as certain differential equations, become easier to solve when the Fourier transform is applied. In that case the solution to the original problem is recovered using the inverse Fourier transform.

• Onfreq i2p.svg

  Real and imaginary parts of integrand for Fourier transform at 3 Hz

• 

  Real and imaginary parts of integrand for Fourier transform at 5 Hz

Related pages

• Fourier analysis
• Fourier inversion theorem
• Fourier series
• Laplace transform

Other websites

• Media related to Fourier transformation at Wikimedia Commons