Graph theory
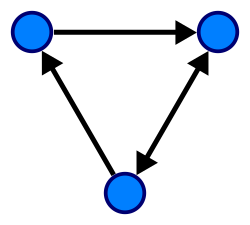
Graph theory is a field of mathematics about graphs. A graph is an abstract representation of: a number of points that are connected by lines. Each point is usually called a vertex (more than one are called vertices), and the lines are called edges. Graphs are a tool for modelling relationships. They are used to find answers to a number of problems.
Some of these questions are:
- What is the best way for a mailman to get to all of the houses in the area in the least amount of time? The points could represent street corners and lines could represent the houses along the street. (see Chinese postman problem)
- A salesman has to visit different customers, but wants to keep the distance traveled as small as possible. The problem is to find a way so they can do it. This problem is known as Travelling Salesman Problem (and often abbreviated TSP). It is among the hardest problems to solve. If a commonly believed conjecture is true (described as P ≠ NP), then an exact solution requires one to try all possible routes to find which is shortest.
- How many colors would be needed to color a map, if countries sharing a border are colored differently? The points could represent the different areas and the lines could represent that two areas are neighboring. (look at the Four color theorem)
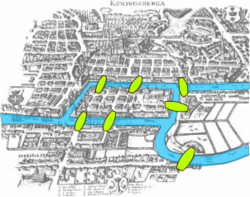
- Can a sketch be drawn in one closed line? The lines of the drawing are the lines of the graph and when two or more lines collide, there is a point in the graph. The task is now to find a way through the graph using each line one time. (look at Seven Bridges of Königsberg)
Different kinds of graphs
- Graph theory has many aspects. Graphs can be directed or undirected. An example of a directed graph would be the system of roads in a city. Some streets in the city are one way streets. This means, that on those parts there is only one direction to follow.
- Graphs can be weighted. An example would be a road network, with distances, or with tolls (for roads).
- The nodes (the circles in the schematic) of a graph are called vertices. The lines connecting the nodes are called edges. There can be no line between two nodes, there can be one line, or there can be multiple lines.
- In graph theory, Trees structures are widely used, they represent hierarchical structures. A Tree is a directed or undirected graph where there is no cycle, meaning: no way of going from one vertex (for example a town) to the same one using each edge you use only once (walking only once on each road you take).
History
A visualization of the Seven Bridges of Königberg. Leonhard Euler solved this problem in 1736, which led to the development of topology, and modern graph theory.
A graph is an abstract data structure. It holds nodes that are usually related to each other. A node is a dataset, typically in the form of ordered pairs. Nodes are either connected or not connected to another node. The relation between nodes is usually defined as an Edge. Graphs are useful for their ability to associate nodes with other nodes. There are a few representations of Graphs in practice.
Leonhard Euler used to live in a town called Königsberg. (Its name changed to Kaliningrad in 1946). The town is on the river Pregel. There is an island in the river. There are some bridges across the river. Euler wanted to walk around and use each of the bridges once. He asked if he could do this. In 1736, he published a scientific article where he showed that this was not possible. Today, this problem is known as the Seven Bridges of Königsberg. The article is seen as the first paper in the history of graph theory.[1]
This article, as well as the one written by Vandermonde on the knight problem, carried on with the analysis situs initiated by Leibniz. Euler's formula was about the number of edges, vertices, and faces of a convex polyhedron was studied and generalized by Cauchy[2] and L'Huillier,[3] and is at the origin of topology.
The fusion of the ideas coming from mathematics with those coming from chemistry is at the origin of a part of the standard terminology of graph theory. In particular, the term "graph" was introduced by Sylvester in an article published in 1878 in Nature.[4]
One of the most famous and productive problems of graph theory is the four color problem: "Is it true that any map drawn in the plane may have its regions colored with four colors, in such a way that any two regions having a common border have different colors?"
Graph theory in perspective
Graph theory is an important part of mathematics and computer science. To many such problems, exact solutions do exist. Many times however, they are very hard to calculate. Therefore, very often, approximations are used. There are two kinds of such approximations, Monte-Carlo algorithms and Las-Vegas algorithms.
Graph Theory Media
References
- ↑ Biggs, N.; Lloyd, E. and Wilson, R. (1986). Graph Theory, 1736-1936. Oxford University Press.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ↑ Cauchy, A.L. (1813). "Recherche sur les polyèdres - premier mémoire". Journal de l'École Polytechnique. 9 (Cahier 16): 66–86.
- ↑ L'Huillier, S.-A.-J. (1861). "Mémoire sur la polyèdrométrie". Annales de Mathématiques. 3: 169–189.
- ↑ Sylvester, J.J. (1878). "Chemistry and Algebra". Nature. 17 (432): 284. Bibcode:1878Natur..17..284S. doi:10.1038/017284a0. S2CID 26451061.