Information entropy

Information theory
Entropy Differential entropy Conditional entropy Joint entropy Mutual information Conditional mutual information Entropy rate
Asymptotic equipartition property Rate–distortion theory
Shannon's source coding theorem Noisy-channel coding theorem

Information entropy is a concept from information theory. It tells how much information there is in an event. In general, the more certain or deterministic the event is, the less information it will contain. More clearly stated, information is an increase in uncertainty or entropy. The concept of information entropy was created by mathematician Claude Shannon.

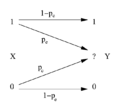
Information and its relationship to entropy can be modeled by:

R = H(x) - Hy(x)

"The conditional entropy Hy(x) will, for convenience, be called the equivocation. It measures the average ambiguity of the received signal."

The "average ambiguity" or Hy(x) meaning uncertainty or entropy. H(x) represents information. R is the received signal.

It has applications in many areas, including lossless data compression, statistical inference, cryptography, and sometimes in other disciplines as biology, physics or machine learning.

The information gain is a measure of the probability with which a certain result is expected to happen. In the context of a coin flip, with a 50-50 probability, the entropy is the highest value of 1. It does not involve information gain because it does not incline towards a specific result more than the other. If there is a 100-0 probability that a result will occur, the entropy is 0.

Example

Let's look at an example. If someone is told something they already know, the information they get is very small. It will be pointless for them to be told something they already know. This information would have very low entropy.

If they were told about something they knew little about, they would get much new information. This information would be very valuable to them. They would learn something. This information would have high entropy.

Information Entropy Media

• 

  Two bits of entropy: In the case of two fair coin tosses, the information entropy in bits is the base-2 logarithm of the number of possible outcomes‍— with two coins there are four possible outcomes, and two bits of entropy. Generally, information entropy is the average amount of information conveyed by an event, when considering all possible outcomes.

Related pages

• Entropy (Information Theory)
• Mutual information
• Thermodynamic entropy
• Entropy
• Claude Shannon

Other websites

• Information is not entropy, ! Archived 2016-12-01 at the Wayback Machine - a discussion of the use of the terms "information" and "entropy".
• I'm confused: how could information equal entropy? - a similar discussion on the bionet.info-theory FAQ.
• Java "entropy pool" for cryptographically-secure unguessable random numbers Archived 2008-12-02 at the Wayback Machine
• Description of information entropy from Tools for thought' by Howard Rheingold
• An intuitive guide to the concept of entropy arising in various sectors of science – a wikibook on the interpretation of the concept of entropy.