Information theory
| Information theory |
|---|
 |
Information theory is a branch of applied mathematics and electrical engineering. Information theory measures the amount of information in data that could have more than one value. In its most common use, information theory finds physical and mathematical limits on the amounts of data in data compression and data communication. Data compression and data communication are statistical, because they guess unknown values. The amount of information in data measures how easily it is guessed by a person who does not know its value.
A key measure in information theory is "entropy". Entropy quantifies the amount of uncertainty involved in the value of a random variable or the outcome of a random process. For example, identifying the outcome of a fair coin flip (with two equally likely outcomes) provides less information (lower entropy) than specifying the outcome from a roll of a dice (with six equally likely outcomes). Some other important measures in information theory are mutual information, channel capacity, error exponents, and relative entropy.
Information Theory Media
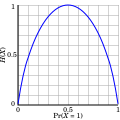
The entropy of a Bernoulli trial as a function of success probability, often called the binary entropy function, Hb(p). The entropy is maximized at 1 bit per trial when the two possible outcomes are equally probable, as in an unbiased coin toss.
A picture showing scratches on the readable surface of a CD-R. Music and data CDs are coded using error correcting codes and thus can still be read even if they have minor scratches using error detection and correction.
A binary symmetric channel. Redrawn from bitmap image en:Image:Binarysymmetricchannel.JPG
A binary erasure channel. Redrawn from bitmap image en:Image:Binaryerasurechannel.JPG
