Least common multiple

The least common multiple of two integers is the smallest positive integer between all the multiples of both. It is usually written as LCM(a, b). Likewise, the LCM of more than two integers is the smallest positive integer that is divisible by each of them.

In elementary arithmetic, the LCM is also the "lowest common denominator" (LCD) that must be calculated, before fractions can be added, subtracted or compared.

Overview

A multiple of a number is the product of that number and an integer. For example, 10 is a multiple of 5 because 5 × 2 = 10, so 10 is divisible by 5 and 2. Because 10 is the smallest positive integer that is divisible by both 5 and 2, it is the least common multiple of 5 and 2. By the same principle, 10 is the least common multiple of 5 and 2 as well.

Relation with the greatest common divisor

It is known that:

[math]\displaystyle{ \operatorname{GCD}(a,b) \cdot \operatorname{LCM}(a,b) = |a \cdot b| }[/math]

where [math]\displaystyle{ \operatorname{GCD}(a,b) }[/math] is the greatest common divisor of a and b, This formula is often used to compute the LCD, by first finding the GCD of a and b.

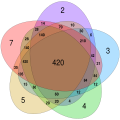
Least Common Multiple Media

• 

  A Venn diagram showing the least common multiples of combinations of 2, 3, 4, 5 and 7 (6 is skipped as it is 2 × 3, both of which are already represented).For example, a card game which requires its cards to be divided equally among up to 5 players requires at least 60 cards, the number at the intersection of the 2, 3, 4, and 5 sets, but not the 7 set.

• 

  Least common multiple

Related pages

• Greatest common divisor