Minkowski spacetime
In special relativity, the Minkowski spacetime is a four-dimensional manifold, created by Hermann Minkowski. It has four dimensions: three dimensions of space (x, y, z) and one dimension of time. Minkowski spacetime has a metric signature of (-+++), and describes a flat space when no mass or energy is present. The convention in this article is to call Minkowski spacetime simply spacetime.
However, Minkowski spacetime only applies in special relativity. General relativity used the notion of curved spacetime to describe the effects of gravity and accelerated motion.
Definition(s)
Mathematical
Spacetime can be thought of as a four-dimensional coordinate system in which the axes are given by
[math]\displaystyle{ (ct, x, y, z) }[/math]
They can also be denoted by
[math]\displaystyle{ (x_1, x_2, x_3, x_4) }[/math]
Where [math]\displaystyle{ x_1 }[/math] represents [math]\displaystyle{ ct }[/math]. The reason for measuring time in units of the speed of light times the time coordinate is so that the units for time are the same as the units for space. Spacetime has the differential for arc length given by
[math]\displaystyle{ ds^2=-c^2dt^2+dx^2+dy^2+dz^2 }[/math]
This implies that spacetime has a metric tensor given by
[math]\displaystyle{ g_{uv}=\begin{bmatrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix} }[/math]
As before stated, spacetime is flat everywhere; to some extent, it can be thought of as a plane.
Simple
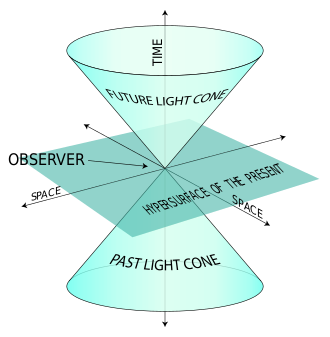
Spacetime can be thought of as the "arena" in which all of the events in the universe take place. All that one needs to specify a point in spacetime is a certain time and a typical spatial orientation. It is very hard to visualize four dimensions, but an analogy can be made, using the method below.
Spacetime diagrams
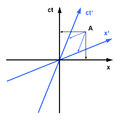
Hermann Minkowski introduced a certain method for graphing coordinate systems in Minkowski spacetime. As seen to the right, different coordinate systems will disagree on an object's spatial orientation and/or position in time. As you can see from the diagram, there is only one spatial axis (the x-axis) and one time axis (the t-axis). It is possibly to introduce an extra spatial dimension, (the y-axis); unfortunately, this is the limit of adding dimensions while still being easy to visualize. It is possible to add the last spatial dimension (the z-axis), however visualizing 4d, while possible, is very hard. The rule for graphing in Minkowski spacetime goes as follows:
1) The angle between the x-axis and the x'-axis is given by [math]\displaystyle{ \tan(\alpha) = \frac{v}{c} }[/math] where v is the velocity of the object.
2) The speed of light through spacetime always makes an angle of 45 degrees with either axis.
In a spacetime diagram, to change your velocity, a Lorentz transform is used, the spacetime equivalent of a rotation. Visually, this looks like a squeeze but rotated 45° (a squeeze-mapping). Importantly, a 45° line won’t change by doing the Lorentz transform, meaning the speed of light is the same for everyone.
Spacetime in general relativity
In the general theory of relativity, Einstein used the equation
[math]\displaystyle{ \mathbb{G}_{mv}=8\pi \mathcal{G} \mathbb{T}_{mv} }[/math]
To allow for spacetime to actually curve; the resulting effects are those of gravity.
Minkowski Spacetime Media
Hermann Minkowski (1864–1909) found that the theory of special relativity could be best understood as a four-dimensional space, since known as the Minkowski spacetime.
A pictorial representation of the tangent space at a point, x, on a sphere. This vector space can be thought of as a subspace of R3 itself. Then vectors in it would be called geometrical tangent vectors. By the same principle, the tangent space at a point in flat spacetime can be thought of as a subspace of spacetime, which happens to be all of spacetime.
The blue axes are hyperbolically-orthogonal; light speed is constant over all such pairs
Linear functionals (1-forms) α, β and their sum σ and vectors u, v, w, in 3d Euclidean space. The number of (1-form) hyperplanes intersected by a vector equals the inner product.
Red circular arc is geodesic in Poincaré disk model; it projects to the brown geodesic on the green hyperboloid.
