Square number

A square number, sometimes also called a perfect square, is the result of an integer multiplied by itself. 1, 4, 9, 16 and 25 are the first five square numbers. In a formula, the square of a number n is denoted n² (exponentiation), usually pronounced as "n squared". The name square number comes from the name of the shape; see below.

Square numbers are non-negative. Another way of saying that a (non-negative) number is a square number, is that its square root is again an integer. For example, √9 = 3, so 9 is a square number.

Examples

The squares (sequence A000290 in OEIS) smaller than 70² are:

0² =0

1² = 1

2² = 4

3² = 9

4² = 16

5² = 25

6² = 36

7² = 49

8² = 64

9² = 81

10² =100

11² = 121

12² = 144

13² = 169

14² = 196

15² = 225

16² = 256

17² = 289

18² = 324

19² = 361

20² = 400

21² = 441

22² = 484

23² = 529

24² = 576

25² = 625

26² = 676

27² = 729

28² = 784

29² = 841

30² = 900

31² = 961

32² = 1024

33² = 1089

34² = 1156

35² = 1225

36² = 1296

37² = 1369

38² = 1444

39² = 1521

40² = 1600

41² = 1681

42² = 1764

43² = 1849

44² = 1936

45² = 2025

46² = 2116

47² = 2209

48² = 2304

49² = 2401

50² = 2500

51² = 2601

52² = 2704

53² = 2809

54² = 2916

55² = 3025

56² = 3136

57² = 3249

58² = 3364

59² = 3481

60² = 3600

61² = 3721

62² = 3844

63² = 3969

64² = 4096

65² = 4225

66² = 4356

67² = 4489

68² = 4624

69² = 4761

There are infinitely many square numbers, as there are infinitely many natural numbers.

Properties

The number m is a square number if and only if one can compose a square of m equal (lesser) squares:

m = 12 = 1
m = 22 = 4
m = 32 = 9
m = 42 = 16
m = 52 = 25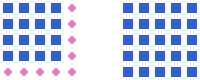
Note: White gaps between squares serve only to improve visual perception. There must be no gaps between actual squares.

A square with side length n has area n².

The expression for the nth square number is n². This is also equal to the sum of the first n odd numbers as can be seen in the above pictures, where a square results from the previous one by adding an odd number of points (shown in magenta). The formula follows:

[math]\displaystyle{ n^2 = \sum_{k=1}^n(2k-1). }[/math]

So for example, 5² =25= 1 + 3 + 5 + 7 + 9.

A square number can end only with digits 0, 1, 4, 6, 9, or 25 in base 10, as follows:

1. If the last digit of a number is 0, its square ends in an even number of 0s (so at least 00) and the digits preceding the ending 0s must also form a square.
2. If the last digit of a number is 1 or 9, its square ends in 1 and the number formed by its preceding digits must be divisible by four.
3. If the last digit of a number is 2 or 8, its square ends in 4 and the preceding digit must be even.
4. If the last digit of a number is 3 or 7, its square ends in 9 and the number formed by its preceding digits must be divisible by four.
5. If the last digit of a number is 4 or 6, its square ends in 6 and the preceding digit must be odd.
6. If the last digit of a number is 5, its square ends in 25 and the preceding digits must be 0, 2, 06, or 56.

A square number cannot be a perfect number.

All fourth powers, sixth powers, eighth powers and so on are perfect squares.

Special cases

• If the number is of the form m5 where m represents the preceding digits, its square is n25 where n = m × (m + 1) and represents digits before 25. For example the square of 65 can be calculated by n = 6 × (6 + 1) = 42 which makes the square equal to 4225.
• If the number is of the form m0 where m represents the preceding digits, its square is n00 where n = m². For example the square of 70 is 4900.
• If the number has two digits and is of the form 5m where m represents the units digit, its square is AABB where AA = 25 + m and BB = m². Example: To calculate the square of 57, 25 + 7 = 32 and 7² = 49, which means 57² = 3249.

Odd and even square numbers

Squares of even numbers are even (and in fact divisible by 4), since (2n)² = 4n².

Squares of odd numbers are odd, since (2n + 1)² = 4(n² + n) + 1.

It follows that square roots of even square numbers are even, and square roots of odd square numbers are odd.

As all even square numbers are divisible by 4, the even numbers of the form 4n + 2 are not square numbers.

As all odd square numbers are of the form 4n + 1, the odd numbers of the form 4n + 3 are not square numbers.

Squares of odd numbers are of the form 8n + 1, since (2n + 1)² = 4n(n + 1) + 1 and n(n + 1) is an even number.

see also

• Square pyramidal number

Square Number Media

• 

  Square number 16 as sum of gnomons.

• 

  Squarenumber

• 

  Squarenumber

• 

  Squarenumber

• 

  Squarenumber

• 

  Squarenumber

• 

  The sum of the first n odd integers is n2. 1 + 3 + 5 + ... + (2n − 1) = n2. Animated 3D visualization on a tetrahedron.

• 

  Proof without words for the sum of odd numbers theorem

References

• Weisstein, Eric W., "Square Number" from MathWorld.

Further reading

• Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 30–32, 1996. ISBN 0-387-97993-X

Other websites

• Learn Square Numbers Archived 2008-02-11 at the Wayback Machine. Practice square numbers up to 144 with this children's multiplication game
• Dario Alpern, Sum of squares. A Java applet to decompose a natural number into a sum of up to four squares.
• Fibonacci and Square Numbers Archived 2007-09-30 at the Wayback Machine at Convergence Archived 2006-02-12 at the Wayback Machine
• The first 1,000,000 perfect squares Includes a program for generating perfect squares up to 10¹⁵.