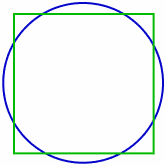
Squaring the circle
Squaring the circle is a problem of geometry. The problem is to construct a square that has the same area as the unit circle, only by using a compass and straightedge construction method. Some people also call this problem the quadrature of the circle.
This is not about a circle with corners like a square. It is a problem like squaring a triangle. It is easy to construct a square with the same area as a triangle. Squaring the circle is related to the other ancient problems which have been proved impossible, squaring the cube and trisecting the angle.
In 1882, Ferdinand von Lindenmann proved that this cannot be done because it is impossible to calculate √π exactly, because it is a transcendental number.
Squaring The Circle Media
Squaring the circle: the areas of this square and this circle are both equal to \pi. In 1882, it was proven that this figure cannot be constructed in a finite number of steps with an idealized compass and straightedge.
Some apparent partial solutions gave false hope for a long time. In this figure, the shaded figure is the lune of Hippocrates. Its area is equal to the area of the triangle ABC (found by Hippocrates of Chios).
Photo of the cover of the book "Carl Theodore Heisel, 1934, Behold! : the grand problem the circle squared beyond refutation no longer unsolved"
- Vitruvian Man
