Strict weak ordering
Strict weak ordering is a binary relation on a set. Such relations define a strict ordering, but they contain several elements of the same type. An example might be the relation "costs less than", or "is cheaper than". For any two elements that are of different types, the relation holds. On the other hand, there are some elements that cannot be ordered that way, because they are of the same type. An example for such a relation may be the relation, costs less than: milk may cost less than bread, and bread may cost less than cake. Two items of different types may cost less than another, but they can otherwise have the same price.
Two different algorithms that sort words by the number of letters in the word may not give the same ordering of the words with the same number of letters, but they will always give an ordering where the four-letter words come before the five-letter-words, and after the three-letter-words.
Time will give a strict weak ordering too; Events that are equivalent in the timeframe happen at the same time.
Strict Weak Ordering Media
A weak order on the set \{a, b, c, d\} where a is ranked below b and c, b and c are of equal rank, and d is ranked above b and c I) representation as a strict weak order \,
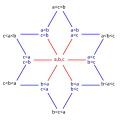
The 13 possible strict weak orderings on a set of three elements \{a, b, c\}. The only total orders are shown in black. Two orderings are connected by an edge if they differ by a single dichotomy.
The permutohedron on four elements, a three-dimensional convex polyhedron. It has 24 vertices, 36 edges, and 14 two-dimensional faces, which all together with the whole three-dimensional polyhedron correspond to the 75 weak orderings on four elements.
