Vector
A vector is a mathematical object that has a size, called the magnitude, and a direction. It is often represented by boldface letters (such as [math]\displaystyle{ \mathbf{u} }[/math], [math]\displaystyle{ \mathbf{v} }[/math], [math]\displaystyle{ \mathbf{w} }[/math]), or as a line segment from one point to another (as in [math]\displaystyle{ \overrightarrow{AB} }[/math]).[1][2]
For example, a vector would be used to show the distance and direction something moved in. When asking for directions, if one says "Walk one kilometer towards the North", that would be a vector, but if they say "Walk one kilometer", without showing a direction, then that would be a scalar.
We usually draw vectors as arrows. The length of the arrow is proportional to the vector's magnitude. The direction in which the arrow points to is the vector's direction.[3]
Examples of vectors
Examples of scalars
- The distance between two places is 10 kilometers. This distance is not a vector because it does not contain a direction.
- The number of fruit in a box is not a vector.
- A person pointing is not a vector because there is only a direction. There is no magnitude (the distance from the person's finger to a building, for example).
- The length of an object.
- A car drives at 100 kilometers per hour. This does not describe a vector, as there is only a magnitude, but no direction.
More examples of vectors
- Displacement is a vector. Displacement is the distance that something moves in a certain direction. A measure of distance alone is a scalar.
- Force that includes direction is a vector.[3]
- Velocity is a vector, because it is a speed in a certain direction.[3][4]
- Acceleration is the rate of change of velocity. An object is accelerating if it is changing speed or changing direction.
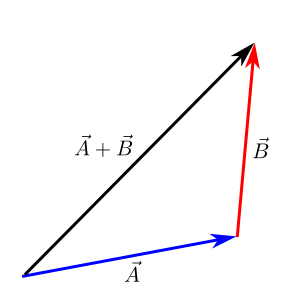
How to add vectors
Adding vectors on paper using the head to tail method
The Head to Tail method of adding vectors is useful for doing an estimate on paper of the result of adding two vectors. To do it:
- Each vector is drawn as an arrow with an amount of length behind it, where each unit of length on the paper represents a certain magnitude of the vector.
- Draw the next vector, with the tail(end) of the second vector at the head(front) of the first vector.
- Repeat for all further vectors: Draw the tail of the next vector at head of the previous one.
- Draw a line from the tail of the first vector to the head of the last vector - that's the resultant(sum) of all the vectors.
It's called the "Head to Tail" method, because each head from the previous vector leads in to the tail of the next one.
Using component form
Using the component form to add two vectors literally means adding the components of the vectors to create a new vector.[5] For example, let a and b be two two-dimensional vectors. These vectors can be written in terms of their components.
[math]\displaystyle{ \mathbf{a} = ( a_x, a_y ) }[/math]
[math]\displaystyle{ \mathbf{b} = ( b_x, b_y ) }[/math]
Suppose c is the sum of these two vectors, so that c = a + b. This means that [math]\displaystyle{ \mathbf{c} = ( a_x + b_x, a_y + b_y ) }[/math].
Here is an example of addition of two vectors, using their component forms:
[math]\displaystyle{ \mathbf{a} = ( 3, -1 ) }[/math]
[math]\displaystyle{ \mathbf{b} = ( 2, 2 ) }[/math]
[math]\displaystyle{ \begin{align}\mathbf{c} & = \mathbf{a} + \mathbf{b} \\ & = ( a_x + b_x, a_y + b_y ) \\ & = ( 3 + 2, -1 + 2 ) \\ & = ( 5, 1 ) \end{align} }[/math]
This method works for all vectors, not just two dimensional ones.
How to multiply vectors
Using the dot product
The dot product is one method to multiply vectors. It produces a scalar. It uses component form:
[math]\displaystyle{ \begin{align}\mathbf{a} & = (2, 3)\\ \mathbf{b} & = (1, 4) \\ \mathbf{a} \cdot \mathbf{b} & = (2,3)\cdot(1,4) \\ & = (2\cdot 1)+(3\cdot 4) \\ & = 2+12 \\ &= 14 \end{align} }[/math]
Using the cross product
The cross product is another method to multiply vectors. Unlike dot product, it produces a vector. Using component form:
[math]\displaystyle{ \mathbf{a}\times\mathbf{b}=|\mathbf{a}||\mathbf{b}|\sin(\theta) \mathbf{n} }[/math]
Here, [math]\displaystyle{ |\mathbf{a}| }[/math] means the length of [math]\displaystyle{ \mathbf{a} }[/math], and [math]\displaystyle{ \mathbf{n} }[/math] is the unit vector at right angles to both [math]\displaystyle{ \mathbf{a} }[/math] and [math]\displaystyle{ \mathbf{b} }[/math].
Multiplying by a scalar
To multiply a vector by a scalar (a normal number), you multiply the number by each component of the vector:
[math]\displaystyle{ c\,\mathbf{x} = (c\,x_1,c\,x_2,...,c\,x_n) }[/math]
An example of this is
[math]\displaystyle{ \begin{align}c & = 5\\ \mathbf{x} & = (3,4)\\ c\,\mathbf{x} & = (5\cdot3, 5\cdot4)\\ & = (15, 20) \end{align} }[/math]
Related pages
References
- ↑ "Comprehensive List of Algebra Symbols". Math Vault. 2020-03-25. Retrieved 2020-08-19.
- ↑ Weisstein, Eric W. "Vector". mathworld.wolfram.com. Retrieved 2020-08-19.
- ↑ 3.0 3.1 3.2 "Vectors". www.mathsisfun.com. Retrieved 2020-08-19.
- ↑ "vector | Definition & Facts". Encyclopedia Britannica. Retrieved 2020-08-19.
- ↑ "1.1: Vectors". Mathematics LibreTexts. 2013-11-07. Retrieved 2020-08-19.