Velocity
Velocity is a measure of how fast something moves in a particular direction. To define it needs both magnitude and direction. If an object moves east at 9 metres per second (9 m/s), then its velocity is 9 m/s to the east.
The idea behind this is that speed does not tell us in which direction the object moves in a given frame of reference. Speed is one part of velocity, direction is the other part. Depending on the frame of reference, the velocity can be defined with many mathematical concepts required for making the correct analysis.
Velocity in one-dimensional motion
Average velocity
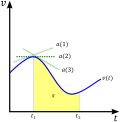
To calculate the average velocity of an object, we divide its displacement (its change of position) by the time it took to change position.
[math]\displaystyle{ {\overrightarrow v_{average}} = \frac\text{displacement}\text{time interval}\Leftrightarrow \overrightarrow v_{average}={\Delta {\overrightarrow r} \over \Delta t}\Leftrightarrow \overrightarrow v_{average}={\overrightarrow r_2- \overrightarrow r_1 \over t_2-t_1} }[/math]
where: [math]\displaystyle{ \Delta r - }[/math]is the total distance traveled in a given time interval [math]\displaystyle{ \Delta t }[/math]. Each of these quantities can be calculated by substracting two different values intertwined within the given quantity, hence [math]\displaystyle{ r_2-r_1, t_2-t_1 }[/math]give the desired [math]\displaystyle{ v={r \over t} }[/math].
Instantaneous velocity
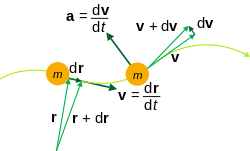
Contrary to average velocity, the instantaneous velocity tells us the rate of change at which a given object is moving along a certain path at a given instance of time, which usually tends to be infinitesimally small.[1]
[math]\displaystyle{ v=\lim_{\Delta t \to 0} {\Delta \overrightarrow r \over \Delta t}\Leftrightarrow v={d \overrightarrow r \over dt} }[/math]
When [math]\displaystyle{ \Delta t \rightarrow 0 }[/math], we can see that [math]\displaystyle{ \Delta r \rightarrow 0 }[/math]. Taking that into consideration we can conceptualize this rate of change between displacement vector and interval of time using mathematical analysis (most notably- Calculus)
Velocity in two-dimensional motion
The concept of velocity allows us to consider two different means of calculating the velocity. Two-dimensional motion requires us to use vector notation to define the physical quantities found throughout the kinematics.
Distinction between average velocity and instantaneous velocity regarding two dimensional motion
Relative velocity
Velocity can also be measured by comparing the motion of two objects. This is called relative velocity. The second object is called the reference frame. To find the relative velocity, subtract the velocity of the reference frame from the velocity of the first object.[2] For example, Earth moves at 67,000 miles per hour around the Sun. Usually, we do not care about this motion. So we subtract the vector that represents Earth's motion from the total motion.[3]
Velocity Media
References
- ↑ Halliday, David. (2013). FUNDAMENTALS OF PHYSICS EXTENDED 10E. Resnick, Robert., Walker, Jearl. (10th ed.). New York: Wiley. ISBN 9781118547878. OCLC 1001998323.
- ↑ "Relative Motion". hyperphysics.phy-astr.gsu.edu. Retrieved 2020-08-31.
- ↑ "How fast is the earth moving?". Scientific American. Retrieved 2020-08-31.