Addition
- Not to be confused with building extensions which are also called additions.
In mathematics, addition, represented by the symbol [math]\displaystyle{ + }[/math], is an operation which combines two mathematical objects together into another mathematical object of the same type, called the sum.[1][2][3] Addition can occur with simple objects such as numbers, and more complex objects and concepts such as vectors and matrices.[4]
Addition has several important properties. It is commutative, meaning that the order of the operands does not matter, and it is associative, meaning that when one adds more than two numbers, the order in which addition is performed does not matter (see Summation). Repeated addition of 1 is the same as counting. Addition of 0 does not change a number. Addition also obeys predictable rules concerning related operations such as subtraction and multiplication.
Arithmetic
In arithmetic, addition is the operation where two or more numbers called "addends" are used to make a new number, which is the "sum" or total that is expressed with the equals sign. The symbol for addition, in infix notation, is the plus sign "+" placed between the operands.

Counting examples
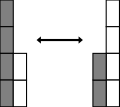
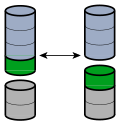
For example, there are objects in two groups (as shown on the right). The objects are various shapes, where one group has 3 of them while the other has 2. When the two groups combine into one, the overall amount (sum) of the shapes become 5.
Vertical Addition
The animation above demonstrates the addition of seven hundred eighty six and four hundred sixty seven. The problem's digits have been separated into units, tens and hundreds (see Place value).
First, the units 6 and 7 are added together to make 13, so 1 ten and 3 units, with the 3 written below and the 1 ten carried to the tens column. Next, in the tens column, the 1, 8, and 6 are added together to make 15 tens, so 1 hundred and 5 tens, with the 5 written below and the 1 hundred carried to the hundreds column. Finally, in the hundreds column, 1, 7, and 4 are added together to make 12 hundreds, so 1 thousand and 2 hundreds, with the 2 written below and the 1 thousand carried to the thousand column. The final answer is thus one thousand two hundred fifty three.
A measurement example
Tom wants to know the distance between his house and Sally's house. Bob's house is 300 m east of Tom's house. Sally's house is 120 m east of Bob's house:
- Tom's house [math]\displaystyle{ \leftarrow }[/math] 300 m [math]\displaystyle{ \rightarrow }[/math] Bob's house [math]\displaystyle{ \leftarrow }[/math] 120 m [math]\displaystyle{ \rightarrow }[/math] Sally's house
The distance from Tom's house to Sally's house can be found by adding the distances already measured. The distance from Tom's house to Bob's house, added to the distance from Bob's house to Sally's house, is the same as the distance from Tom's house to Sally's house. That is, 300 m plus 120 m.
- [math]\displaystyle{ 300+120=420 }[/math]
Hence Sally's house is 420 m to the east of Tom's house.
Properties
Commutativity
Addition is commutative, meaning that one can change the order of the numbers in a sum, but still get the same result. For example:
- [math]\displaystyle{ 4+5=9 }[/math] and [math]\displaystyle{ 5+4=9 }[/math]
Associativity
Addition is also associative, which means that when three or more numbers are added together, the order of operations does not change the result.
For any three numbers [math]\displaystyle{ a }[/math], [math]\displaystyle{ b }[/math], and [math]\displaystyle{ c }[/math], it is true that [math]\displaystyle{ 1=(a+b)+c=a+(b+c) }[/math]. For example, [math]\displaystyle{ 1=(1+2)+3=3+3=6 }[/math] and [math]\displaystyle{ 1=1+(2+3)=1+5=6 }[/math], which means that [math]\displaystyle{ 1=(1+2)+3=1+(2+3) }[/math].
When addition is used together with other operations, the order of operations becomes important. In the standard order of operations, addition is to be computed later than exponentiation, roots, multiplication and division, but has equal importance as subtraction.[5]
Addition table
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
AdditionAddition Table Media
3 + 2 = 5 with apples, a popular choice in textbooks
An addition with carry
Addition with an op-amp. See Summing amplifier for details.
Related pages
References
- ↑ "List of Arithmetic and Common Math Symbols". Math Vault. 2020-03-17. Retrieved 2020-08-26.
- ↑ "Addition". www.mathisfun.com. Retrieved 2020-08-26.
- ↑ Weisstein, Eric W. "Addition". mathworld.wolfram.com. Retrieved 2020-08-26.
- ↑ "Comprehensive List of Algebra Symbols". Math Vault. 2020-03-25. Retrieved 2020-08-26.
- ↑ Bronstein, Ilja Nikolaevič; Semendjajew, Konstantin Adolfovič (1987) [1945]. "2.4.1.1.". In Grosche, Günter; Ziegler, Viktor; Ziegler, Dorothea (eds.). Taschenbuch der Mathematik (in Deutsch). Vol. 1. Translated by Ziegler, Viktor. Weiß, Jürgen (23 ed.). Thun and Frankfurt am Main: Verlag Harri Deutsch (and B.G. Teubner Verlagsgesellschaft, Leipzig). pp. 115–120. ISBN 978-3-87144-492-0.