Angular momentum

The angular momentum of the figure skater is conserved—as she decreases her radius by retracting her arms and legs, her moment of inertia decreases, but her angular velocity increases to compensate.

The angular momentum or rotational momentum (L) of an object rotating about an axis is the product of its moment of inertia and its angular velocity:

[math]\displaystyle{ L = I \omega }[/math]

where

[math]\displaystyle{ I }[/math] is the moment of inertia (resistance to angular acceleration or deceleration, equal to the product of the mass and the square of its radius measured perpendicularly from the axis of rotation);

[math]\displaystyle{ \omega \ }[/math] is the angular velocity.

There are three kinds of angular momentum: the vibrational angular momentum, the spin angular momentum and the orbital angular momentum.

Vibrational angular momentum

The vibrational angular momentum is that of photons. Its minimum portion is the Planck quantum of vibration or action:

According to this picture, the creation of photons is to be viewed like the plucking of a guitar—as a sudden increment in the excitation of one of the modes of vibration.

—Davies, Paul. The Forces of Nature CUP, 1979, p. 116
... to an energy quantum of vibration, such as that of Planck, there must correspond an energy quantum of rotation ...

—Birtwistle, George. The Quantum Theory of the Atom CUP, 2015, pp. 2–3
The Planck quantum of action, h, has precisely the dimensions of an angular momentum ...

—Biedenharn, L. C.; Louck, J. D. Angular Momentum in Quantum Physics Addison-Wesley Pub. Co., Advanced Book Program, 1981

Spin angular momentum

The spin angular momentum is that of an object turning around an axis which passes through the object's centre (for example, a top spinning around its central axis).

An object that is very spread-out from the axis of rotation has a large moment of inertia—it is very hard to make it start spinning, but once it gets going, it is very hard to make it stop. Similarly, it is easier to make an object start spinning at a low angular velocity than to make it start spinning at a high angular velocity. This is why the spin angular momentum depends both on how spread-out the object is (moment of inertia) and how fast it is spinning (angular velocity).

Orbital angular momentum

The orbital angular momentum is that of an object revolving around an axis which does not pass through the object's centre. For example, the Sun and the Earth orbit each other by revolving around an axis that passes through the Sun, but not through the Sun's centre. The orbital angular momentum measures how hard it would be to make the object stop revolving around the axis.

Conservation

Angular momentum is a conserved quantity—an object's angular momentum stays constant unless an external torque acts on it.

Angular momentum has both a direction and a magnitude, and both are conserved. Bicycles, frisbees and rifle bullets all owe their useful properties to conservation of angular momentum. Conservation of angular momentum is also why cyclones are spiral and neutron stars are rapidly spinning.

Angular MomentumRotational Energy Media

Velocity of the particle m with respect to the origin O can be resolved into components parallel to (v∥) and perpendicular to (v⊥) the radius vector r. The angular momentum of m is proportional to the perpendicular component v⊥ of the velocity, or equivalently, to the perpendicular distance r⊥ from the origin.
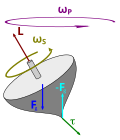
Relationship between force (F), torque (τ), momentum (p), and angular momentum (L) vectors in a rotating system. r is the position vector.
Moment of inertia (shown here), and therefore angular momentum, is different for each shown configuration of mass and axis of rotation.
The torque caused by the two opposing forces Fg and −Fg causes a change in the angular momentum L in the direction of that torque (since torque is the time derivative of angular momentum). This causes the top to precess.
The angular momentum of the particles i is the sum of the cross products R × MV + Σri × mivi.
The 3-angular momentum as a bivector (plane element) and axial vector, of a particle of mass m with instantaneous 3-position x and 3-momentum p.
In this standing wave on a circular string, the circle is broken into exactly 8 wavelengths. A standing wave like this can have 0, 1, 2, or any integer number of wavelengths around the circle, but it cannot have a non-integer number of wavelengths like 8.3. In quantum mechanics, angular momentum is quantized for a similar reason.
Video: A gyroscopic exercise tool is an application of the conservation of angular momentum for muscle strengthening. A mass quickly rotating about its axis in a ball-shaped device defines an angular momentum. When the person exercising tilts the ball, a force results which even increases the rotational speed when reacted to specifically by the user.

Related pages

Other websites

Conservation of angular momentum Archived 2010-12-14 at the Wayback Machine