Cardinality
In mathematics, the cardinality of a set means the number of its elements. For example, the set A = {2, 4, 6} contains 3 elements, and therefore A has a cardinality of 3. The cardinality of a set A can also be represented as [math]\displaystyle{ |A| }[/math].[1][2]
Two sets have the same (or equal) cardinality if and only if they have the same number of elements, which is the another way of saying that there is a 1-to-1 correspondence between the two sets.[3] The cardinality of the set A is less than or equal to the cardinality of set B if and only if there is an injective function from A to B. The cardinality of the set B is greater than or equal to the cardinality of set A if and only if there is an injective function from A to B.
The cardinality of a set is only one way of giving a number to the size of a set. The concept of measure is yet another way.
Notation
||A|| is the cardinality of the set A. Single vertical bars can also be placed around a set to mean cardinality, such as |A|.[1][2]
Finite sets
The cardinality of a finite set is a natural number. The smallest cardinality is 0. The empty set has cardinality 0. If the cardinality of the set A is n, then there is a "next larger" set with cardinality n+1 (for example, the set A ∪ {A}). If ||A|| ≤ ||B|| ≤ ||A ∪ {A}||, then either ||B|| = ||A|| or ||B|| = ||A ∪ {A}||.) There is no largest finite cardinality.
Infinite sets
If the cardinality of a set is not finite, then the cardinality is infinite.[4]
An infinite set is considered countable if they can be listed without missing any (that is, if there is a one-to-one correspondence between it and the set of natural numbers [math]\displaystyle{ \mathbb{N} }[/math]).[3] Examples include the rational numbers, integers, and natural numbers. Such sets have a cardinality that we call [math]\displaystyle{ \aleph_0 }[/math] (pronounced "aleph null", "aleph naught" or "aleph zero"). Sets such as the real numbers are not countable, since given any finite or infinite list of real numbers, it's always possible to find a number that's not on that list. The real numbers have a cardinality of [math]\displaystyle{ \mathfrak{c} }[/math]—the cardinality of the continuum.[1]
Cardinality Media
Georg Cantor, c. 1870
A one-to-one correspondence from N, the set of all non-negative integers, to the set E of non-negative even numbers. Although E is a proper subset of N, both sets have the same cardinality.
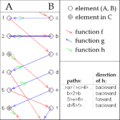
Gyula Kőnig's definition of a bijection h:A → B from the given injections f:A → B and g:B → A.
Algebraic numbers on the complex plane, colored by degree
Visual representation of Hilbert's hotel. Each guest goes to the room with a number that is double their room number, leaving the odd-numbered rooms vacant.
A bijective function, f: X \to Y from the set X = {1,2,3,4} to the set Y demonstrates that Y has cardinality 4.
Related pages
Notes and References
- ↑ 1.0 1.1 1.2 "Comprehensive List of Set Theory Symbols". Math Vault. 2020-04-11. Retrieved 2020-08-23.
- ↑ 2.0 2.1 "Cardinality | Brilliant Math & Science Wiki". brilliant.org. Retrieved 2020-08-23.
- ↑ 3.0 3.1 "Infinite Sets and Cardinality". Mathematics LibreTexts. 2019-12-05. Retrieved 2020-08-23.
- ↑ In order to simplify, we will assume the Axiom of choice