Exclusive disjunction

|
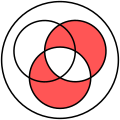
| Venn diagram of [math]\displaystyle{ \scriptstyle A \oplus B }[/math] |

|
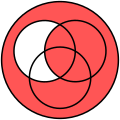
| Venn diagram of [math]\displaystyle{ \scriptstyle A \oplus B \oplus C }[/math]
|
Exclusive disjunction (also called exclusive or, XOR) is a logic operation on two values. It is often represented by the symbol [math]\displaystyle{ \veebar }[/math] (or [math]\displaystyle{ \oplus }[/math]).[1] It will be true, if exactly one of the two values is true. Otherwise, it will be false. This also means that the result of 'XOR' will be true precisely both the values are different. Same values will result in a false.[2]
The best way to remember a XOR operation is: "One or the other, but not both".
Because of that, this is different from inclusive disjunction.[3]
Truth table
The truth table of [math]\displaystyle{ p\, \mathrm{XOR}\, q }[/math] (also written as [math]\displaystyle{ p \oplus q }[/math], [math]\displaystyle{ p \veebar q }[/math],[1] or [math]\displaystyle{ p \neq q }[/math]) is as follows:[2]
| p | q | ⊕ |
|---|---|---|
| F | F | F |
| F | T | T |
| T | F | T |
| T | T | F |
Exclusive Disjunction Media
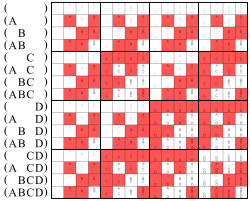
Each row of this binary Walsh matrix is the truth table of the variadic XOR of the arguments shown on the left. E.g. row AB corresponds to the 2-circle, and row ABC to the 3-circle Venn diagram shown above. (As in the Venn diagrams, white is false, and red is true.)
Related pages
References
- ↑ 1.0 1.1 "Comprehensive List of Logic Symbols". Math Vault. 2020-04-06. Retrieved 2020-09-03.
- ↑ 2.0 2.1 Weisstein, Eric W. "XOR". mathworld.wolfram.com. Retrieved 2020-09-03.
- ↑ "Disjunction | logic". Encyclopedia Britannica. Retrieved 2020-09-03.