Icosahedron
An icosahedron is a polyhedron (a three dimensional shape) that is made of triangles and has twenty sides.
There are many kinds of icosahedra, with some being more symmetrical than others. The best known is the regular icosahedron, a Platonic solid made of equilateral triangles.
Regular icosahedra
 Convex regular icosahedron |
 Great icosahedron |
There are two objects, one convex and one concave, that can both be called regular icosahedra. Each has 30 edges and 20 equilateral triangle faces with five meeting at each of its twelve vertices. Both have the same symmetry so that their vertices are at similar places. The term "regular icosahedron" usually refers to the convex icosahedron, while the nonconvex form is called a great icosahedron.
Convex regular icosahedron
The convex regular icosahedron is usually simply called the regular icosahedron. It is one of the five regular Platonic solids, and it is represented by its Schläfli symbol {3, 5}, containing 20 triangular faces, with 5 faces meeting around each vertex.
Its dual polyhedron is the regular dodecahedron {5, 3} which has three regular pentagonal faces around each vertex.
Great icosahedron
The great icosahedron is one of the four regular star Kepler-Poinsot polyhedra. Its Schläfli symbol is [math]\displaystyle{ \{3,\frac52\} }[/math]. Like the convex form, it also has 20 equilateral triangle faces, but its vertex figure is a pentagram rather than a pentagon, leading to geometrically intersecting faces. The intersections of the triangles do not represent new edges.
Its dual polyhedron is the great stellated dodecahedron ([math]\displaystyle{ \frac52,3 }[/math]), having three regular star pentagonal faces around each vertex.
Stellated icosahedra
Stellation is the process of extending the faces or edges of a polyhedron until they meet to form a new polyhedron. It is done symmetrically so that the resulting figure retains the overall symmetry of the parent figure.
In their book The Fifty-Nine Icosahedra, Coxeter et al. enumerated 58 such stellations of the regular icosahedron.
Of these, many have a single face in each of the 20 face planes and so are also icosahedra. The great icosahedron is among them.
Other stellations have more than one face in each plane or form compounds of simpler polyhedra. These are not strictly icosahedra, although they are often referred to as such.
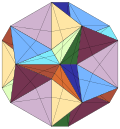
| Notable stellations of the icosahedron | |||||||||
| Regular | Uniform duals | Regular compounds | Regular star | Others | |||||
| (Convex) icosahedron | Small triambic icosahedron | Medial triambic icosahedron | Great triambic icosahedron | Compound of five octahedra | Compound of five tetrahedra | Compound of ten tetrahedra | Great icosahedron | Excavated dodecahedron | Final stellation |
|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
| The stellation process on the icosahedron creates a number of related polyhedra and compounds with icosahedral symmetry. | |||||||||
Icosahedron Media
Convex regular icosahedron
A tensegrity icosahedron
Three interlocking golden rectangles inscribed in a convex regular icosahedron
Pseudoicosahedron net
Icosahedron in cuboctahedron
Icosahedron in cuboctahedron net
Construction from the vertices of a truncated octahedron, showing internal rectangles.
Jessen's icosahedron
Progressions between an octahedron, pseudoicosahedron, and cuboctahedron. The cuboctahedron can flex this way even if its edges (but not its faces) are rigid.
