Triangle
A triangle, otherwise known as a trigon, is a shape, or a part of two dimensional space. It has three straight sides and three vertices. The three angles of a triangle always add up to 180° (180 degrees). It is the polygon with the least possible number of sides. A triangle with vertices A, B, C is written as [math]\displaystyle{ \triangle ABC }[/math].[1][2] The study of geometry related to triangles is called trigonometry. Modern computers usually use triangles to make more complex graphic images or shapes.
Types of triangles
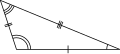
Triangles can be grouped according to how many of their sides are equal:[3]
- if all the three sides of a triangle have the same length, then it is an equilateral triangle.
- if a triangle has two sides with the same length, then it is an isosceles triangle.
- if all the three sides of a triangle have different lengths, then we have a scalene triangle.
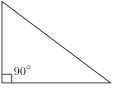
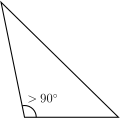
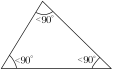
Triangles can also be grouped by their angles:[3]
- if a triangle has a right angle, that is, if one of the angles of that triangle measures 90° (90 degrees), then it is a right triangle. The opposite side to the right angle is the hypotenuse.
- if a triangle has an obtuse angle, that is, if one of the angles of that triangle is larger than 90°, then it is an obtuse triangle.
- if a triangle has only acute angles, that is, if all the angles of that triangle are less than 90°, then it is an acute triangle.
|
|
Area
The area of a triangle is equal to base times height times one half.
[math]\displaystyle{ area= \frac{base \times height}{2} }[/math]
Triangle Media
A triangular bipyramid can be constructed by attaching two tetrahedra. This polyhedron can be said to be a simplicial polyhedron because all of its faces are triangles. More specifically, when the faces are equilateral, it is categorized as a deltahedron.
Orange triangles △ABC share a base AB and area. The locus of their apex C is a line (dashed green) parallel to the base. This is the Euclidean version of Lexell's theorem.
The Calabi triangle and the three placements of its largest square. The placement on the long side of the triangle is inscribed; the other two are not.
Related pages
References
- ↑ "List of Geometry and Trigonometry Symbols". Math Vault. 2020-04-17. Retrieved 2020-09-01.
- ↑ Weisstein, Eric W. "Triangle". mathworld.wolfram.com. Retrieved 2020-09-01.
- ↑ 3.0 3.1 "Triangles - Equilateral, Isosceles and Scalene". www.mathsisfun.com. Retrieved 2020-09-01.
+{{{1}}}−{{{2}}}