KidzSearch Wiki

Polygon

Polygons: open (excluding its boundary), boundary only (excluding interior), closed (including both boundary and interior), and self-intersecting

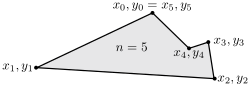
A polygon is a closed two-dimensional shape. It is a simple curve that is made up of straight line segments. It usually has three sides and three corners or more.

It could also be referred to as 'A closed plane figure bound by three or more straight line segments'. It has a number of sides, also called edges. A square is a polygon because it has four sides. The smallest possible polygon in a Euclidean geometry or "flat geometry" is the triangle, but on a sphere, there can be a digon and a henagon.

If the edges (lines of the polygon) do not intersect (cross each other), the polygon is called simple, otherwise it is complex.

In computer graphics, polygons (especially triangles) are often used to make graphics.

Gallery

  • A complex pentagon

  • A simple concave hexagon

  • A non-regular heptagon

  • A non-regular octagon

  • A non-regular decagon

  • A enneacontakaienneagon

The List of polygons

Polygon names and miscellaneous properties
Name Sides Properties
monogon 1 Not generally recognised as a polygon,[1] although some disciplines such as graph theory sometimes use the term.[2]
digon 2 Not generally recognised as a polygon in the Euclidean plane, although it can exist as a spherical polygon.[3]
triangle (or trigon) 3 The simplest polygon which can exist in the Euclidean plane. Can tile the plane.
quadrilateral (or tetragon) 4 The simplest polygon which can cross itself; the simplest polygon which can be concave; the simplest polygon which can be non-cyclic. Can tile the plane.
pentagon 5 [4] The simplest polygon which can exist as a regular star. A star pentagon is known as a pentagram or pentacle.
hexagon 6 [4] Can tile the plane.
heptagon (or septagon) 7 [4] The simplest polygon such that the regular form is not constructible with compass and straightedge. However, it can be constructed using a Neusis construction.
octagon 8 [4]
enneagon (or nonagon) 9 [4]"Nonagon" mixes Latin [novem = 9] with Greek; "enneagon" is pure Greek.
decagon 10 [4]
hendecagon (or undecagon) 11 [4] The simplest polygon such that the regular form cannot be constructed with compass, straightedge, and angle trisector.
dodecagon (or duodecagon) 12 [4]
tridecagon (or trisdecagon) 13 [4]
tetradecagon 14 [4]
pentadecagon (or quindecagon) 15 [4]
hexadecagon (or hekkaidecagon) 16 [4]
heptadecagon (or septadecagon) 17 Constructible polygon
octadecagon 18 [4]
enneadecagon (or Nona decagon) 19 [4]
icosagon 20 [4]
icositetragon (or icosikaitetragon) 24 [4]
triacontagon 30 [4]
tetracontagon (or tessaracontagon) 40 [4][5]
pentacontagon (or pentecontagon) 50 [4][5]
hexacontagon (or hexecontagon) 60 [4][5]
heptacontagon (or hebdomecontagon) 70 [4][5]
octacontagon (or ogdoëcontagon) 80 [4][5]
enneacontagon (or enenecontagon) 90 [4][5]
hectogon (or hecatontagon) 100 [4]
257-gon 257 Constructible polygon
chiliagon 1,000 Philosophers including René Descartes,[6] Immanuel Kant,[7] David Hume,[8] have used the chiliagon as an example in discussions.
myriagon 10,000 Used as an example in some philosophical discussions, for example in Descartes's Meditations on First Philosophy
65,537-gon 65,537 Constructible polygon
megagon[9][10][11] 1,000,000 As with René Descartes's example of the chiliagon, the million-sided polygon has been used as an illustration of a well-defined concept that cannot be visualised.[12][13][14][15][16][17][18] The megagon is also used as an illustration of the convergence of regular polygons to a circle.[19]
apeirogon ∞ A degenerate polygon of infinitely many sides.

References

  1. ↑ Grunbaum, B.; "Are your polyhedra the same as my polyhedra", Discrete and computational geometry: the Goodman-Pollack Festschrift, Ed. Aronov et al., Springer (2003), p. 464.
  2. ↑ Hass, Joel; Morgan, Frank (1996), "Geodesic nets on the 2-sphere", Proceedings of the American Mathematical Society, 124 (12): 3843–3850, doi:10.1090/S0002-9939-96-03492-2, JSTOR 2161556, MR 1343696.
  3. ↑ Coxeter, H.S.M.; Regular polytopes, Dover Edition (1973), p. 4.
  4. ↑ 4.00 4.01 4.02 4.03 4.04 4.05 4.06 4.07 4.08 4.09 4.10 4.11 4.12 4.13 4.14 4.15 4.16 4.17 4.18 4.19 4.20 4.21 4.22 4.23 Salomon, David (2011). The Computer Graphics Manual. Springer Science & Business Media. pp. 88–90. ISBN 978-0-85729-886-7.
  5. ↑ 5.0 5.1 5.2 5.3 5.4 5.5 The New Elements of Mathematics: Algebra and Geometry by Charles Sanders Peirce (1976), p.298
  6. ↑ Sepkoski, David (2005). "Nominalism and constructivism in seventeenth-century mathematical philosophy" (PDF). Historia Mathematica. 32: 33–59. doi:10.1016/j.hm.2003.09.002. Archived from the original (PDF) on 12 May 2012. Retrieved 18 April 2012.
  7. ↑ Gottfried Martin (1955), Kant's Metaphysics and Theory of Science, Manchester University Press, p. 22.
  8. ↑ David Hume, The Philosophical Works of David Hume, Volume 1, Black and Tait, 1826, p. 101.
  9. ↑ Gibilisco, Stan (2003). Geometry demystified (Online-Ausg. ed.). New York: McGraw-Hill. ISBN 978-0-07-141650-4.
  10. ↑ Darling, David J., The universal book of mathematics: from Abracadabra to Zeno's paradoxes, John Wiley & Sons, 2004. p. 249. ISBN 0-471-27047-4.
  11. ↑ Dugopolski, Mark, College Algebra and Trigonometry, 2nd ed, Addison-Wesley, 1999. p. 505. ISBN 0-201-34712-1.
  12. ↑ McCormick, John Francis, Scholastic Metaphysics, Loyola University Press, 1928, p. 18.
  13. ↑ Merrill, John Calhoun and Odell, S. Jack, Philosophy and Journalism, Longman, 1983, p. 47, ISBN 0-582-28157-1.
  14. ↑ Hospers, John, An Introduction to Philosophical Analysis, 4th ed, Routledge, 1997, p. 56, ISBN 0-415-15792-7.
  15. ↑ Mandik, Pete, Key Terms in Philosophy of Mind, Continuum International Publishing Group, 2010, p. 26, ISBN 1-84706-349-7.
  16. ↑ Kenny, Anthony, The Rise of Modern Philosophy, Oxford University Press, 2006, p. 124, ISBN 0-19-875277-6.
  17. ↑ Balmes, James, Fundamental Philosophy, Vol II, Sadlier and Co., Boston, 1856, p. 27.
  18. ↑ Potter, Vincent G., On Understanding Understanding: A Philosophy of Knowledge, 2nd ed, Fordham University Press, 1993, p. 86, ISBN 0-8232-1486-9.
  19. ↑ Russell, Bertrand, History of Western Philosophy, reprint edition, Routledge, 2004, p. 202, ISBN 0-415-32505-6.


Retrieved from "https://wiki.kidzsearch.com/w/index.php?title=Polygon&oldid=5107536"