Hexadecagon
An hexadecagon or hexakaidecagon is a shape with 16 sides and 16 corners.
| Regular hexadecagon | |
|---|---|
 A regular hexadecagon | |
| Type | Regular polygon |
| Edges and vertices | 16 |
| Schläfli symbol | {16}, t{8}, tt{4} |
| Coxeter diagram |     |
| Symmetry group | Dihedral (D16), order 2×16 |
| Internal angle (degrees) | 157.5° |
| Dual polygon | Self |
| Properties | Convex, cyclic, equilateral, isogonal, isotoxal |
Regular hexadecagon
A regular hexadecagon is a hexadecagon in which all angles are equal and all sides are congruent. Its Schläfli symbol is {16} and can be constructed as a truncated octagon, t{8}, and a twice-truncated square tt{4}. A truncated hexadecagon, t{16}, is a triacontadigon, {32}.
Area
The area of a regular hexadecagon with edge length t is
- [math]\displaystyle{ \begin{align} A = 4t^2 \cot \frac{\pi}{16} =& 4t^2 \left(1+\sqrt{2}+\sqrt{ 4+2\sqrt{2} }\right)\\ =& 4t^2 (\sqrt{2}+1)(\sqrt{4-2\sqrt{2}}+1) .\end{align} }[/math]
Because the hexadecagon has a number of sides that is a power of two, its area can be computed in terms of the circumradius R by truncating Viète's formula:
- [math]\displaystyle{ A=R^2\cdot\frac{2}{1}\cdot\frac{2}{\sqrt{2}}\cdot\frac{2}{\sqrt{2+\sqrt{2}}}=4R^2\sqrt{2-\sqrt{2}}. }[/math]
Since the area of the circumcircle is [math]\displaystyle{ \pi R^2, }[/math] the regular hexadecagon fills approximately 97.45% of its circumcircle.
Dissection
Coxeter states that every parallel-sided 2m-gon can be divided into m(m-1)/2 rhombs. For the regular hexadecagon, m=8, and it can be divided into 28: 4 squares and 3 sets of 8 rhombs. This decomposition is based on a Petrie polygon projection of a 8-cube, with 28 of 1792 faces. [1] The list A006245 enumerates the number of solutions as 1232944, including up to 16-fold rotations and chiral forms in reflection.
|
|
Skew hexadecagon
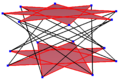
| {8}#{ } | { 8⁄3 }#{ } | { 8⁄5 }#{ } |
|---|---|---|
|
|
|
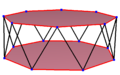
| A regular skew hexadecagon is seen as zig-zagging edges of a octagonal antiprism, a octagrammic antiprism, and a octagrammic crossed-antiprism. | ||
A skew hexadecagon is a skew polygon with 24 vertices and edges but not existing on the same plane. The interior of such an hexadecagon is not generally defined. A skew zig-zag hexadecagon has vertices alternating between two parallel planes.
A regular skew hexadecagon is vertex-transitive with equal edge lengths. In 3-dimensions it will be a zig-zag skew hexadecagon and can be seen in the vertices and side edges of a octagonal antiprism with the same D8d, [2+,16] symmetry, order 32. The octagrammic antiprism, s{2,16/3} and octagrammic crossed-antiprism, s{2,16/5} also have regular skew octagons.
In art
_-_WGA18625.jpg)
In the early 16th century, Raphael was the first to construct a perspective image of a regular hexadecagon: the tower in his painting The Marriage of the Virgin has 16 sides, elaborating on an eight-sided tower in a previous painting by Pietro Perugino.[2]
Hexadecagrams (16-sided star polygons) are included in the Girih patterns in the Alhambra.[3]
Irregular hexadecagons
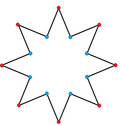
An octagonal star can be seen as a concave hexadecagon:
Hexadecagon Media
en:hexadecagon symmetries
en:16-cube projection in A15 Coxeter plane
16-gon rhombic dissection-size2
Isotoxal 20-gon rhombic dissection-size2
16-gon rhombic dissection2
16-gon rhombic dissectionx
en:regular polygon dissection by rhombi, random
References
- ↑ Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141
- ↑ Speiser, David (2011), "Architecture, mathematics and theology in Raphael's paintings", in Williams, Kim (ed.), Crossroads: History of Science, History of Art. Essays by David Speiser, vol. II, Springer, pp. 29–39, doi:10.1007/978-3-0348-0139-3_3. Originally published in Nexus III: Architecture and Mathematics, Kim Williams, ed. (Ospedaletto, Pisa: Pacini Editore, 2000), pp. 147–156.
- ↑ Hankin, E. Hanbury (May 1925), "Examples of methods of drawing geometrical arabesque patterns", The Mathematical Gazette, 12 (176): 370–373, doi:10.2307/3604213, JSTOR 3604213, S2CID 250431566.