Mandelbrot set
The Mandelbrot set is an example of a fractal in mathematics. It is named after Benoît Mandelbrot, a Polish-French-American mathematician. The Mandelbrot set is important for chaos theory. The edging of the set shows a self-similarity, which is perfect, but because of the minute detail, it looks like it evens out.
The Mandelbrot set can be explained with the equation [math]\displaystyle{ z_{n+1} = z^{\ \, 2}_n + c }[/math]. In that equation, [math]\displaystyle{ c }[/math] and [math]\displaystyle{ z }[/math] are complex numbers and [math]\displaystyle{ n }[/math] is zero or a positive integer (natural number). Starting with [math]\displaystyle{ z_0 = 0 }[/math], [math]\displaystyle{ c }[/math] is in the Mandelbrot set if the absolute value of [math]\displaystyle{ z_n }[/math] never becomes larger than a certain number (that number depends on [math]\displaystyle{ c }[/math]), no matter how large [math]\displaystyle{ n }[/math] gets.
Mandelbrot was one of the first to use computer graphics to create and display fractal geometric images, leading to his discovering the Mandelbrot set in 1979. That was because he had access to IBM's computers. He was able to show how visual complexity can be created from simple rules. He said that things typically considered to be "rough", a "mess" or "chaotic", like clouds or shorelines, actually had a "degree of order". The equation [math]\displaystyle{ z_{n+1} = z^{\ \, 2}_n + c }[/math] was known long before Benoit Mandelbrot used a computer to visualize it.
Images are created by applying the equation to each pixel in an iterative process, using the pixel's position in the image for the number 'c'. 'c' is obtained by mapping the position of the pixel in the image relative to the position of the point on the complex plane.
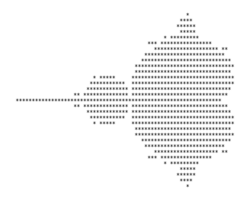
The shape of the Mandelbrot Set is represented in black in the image on this page.
For example, if [math]\displaystyle{ c = 1 }[/math] then the sequence is [math]\displaystyle{ 0,1,2,5,26,\ldots }[/math] which goes to infinity. Therefore, 1 is not an element of the Mandelbrot set, and thus is not coloured black.
On the other hand, if [math]\displaystyle{ c }[/math] is equal to the square root of -1, also known as i, then the sequence is [math]\displaystyle{ 0,i,(-1+i),-i,(-1+i),-i,\ldots }[/math] which does not go to infinity and so it belongs to the Mandelbrot set.
When graphed to show the entire Set, the resultant image is striking, pretty, and quite recognizable.
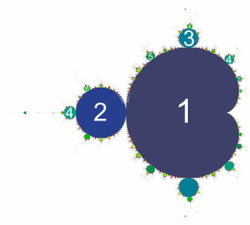
There are many variations of the Mandelbrot set, such as Multibrot, Buddhabrot, and Nebulabrot.
Multibrot is a generalization that allows any exponent: [math]\displaystyle{ z_{n+1} = z^{\ \, d}_n + c }[/math]. These sets are called Multibrot sets. The Multibrot set for d = 2 is the Mandelbrot set.
Mandelbrot Set Media
The Mandelbrot set within a continuously colored environment
Zooming into the boundary of the Mandelbrot set
The first published picture of the Mandelbrot set, by Robert W. Brooks and Peter Matelski in 1978
Correspondence between the Mandelbrot set and the bifurcation diagram of the logistic map
With z_{n} iterates plotted on the vertical axis, the Mandelbrot set can be seen to bifurcate at the period-2k components.
External rays of wakes near the period 1 continent in the Mandelbrot set
Periods of hyperbolic components
Attracting cycle in 2/5-bulb plotted over Julia set (animation)
Attracting cycles and Julia sets for parameters in the 1/2, 3/7, 2/5, 1/3, 1/4, and 1/5 bulbs
Centers of 983 hyperbolic components of the Mandelbrot set.
