Complex number
A complex number is a number, but is different from common numbers in many ways. A complex number is made up using two numbers combined. The first part is a real number, and the second part is an imaginary number. The most important imaginary number is called [math]\displaystyle{ i }[/math], defined as a number that will be -1 when squared ("squared" means "multiplied by itself"): [math]\displaystyle{ i^2 = i \times i = -1\ }[/math]. All other imaginary numbers are [math]\displaystyle{ i }[/math] multiplied by a real number, in the same way that all real numbers can be thought of as 1 multiplied by another number. Arithmetic functions such as addition, subtraction, multiplication, and division can also be performed with complex numbers. They follow commutative, associative and distributive properties, just like real numbers. The set of complex numbers is often represented using the symbol [math]\displaystyle{ \mathbb{C} }[/math].[1][2]
Complex numbers were discovered while attempting to solve special equations that have exponents in them. These equations began to pose problems for mathematicians. As a comparison, using negative numbers, it is possible to find the x in the equation [math]\displaystyle{ a + x = b }[/math] for all real values of a and b, but if only positive numbers are allowed for x, it is sometimes impossible to find a positive x, as in the equation [math]\displaystyle{ 3+x=1 }[/math].
With exponentiation, there is a difficulty to be overcome.[3] There is no real number that gives −1 when it is squared. In other words, −1 (or any other negative number) has no real square root. For example, there is no real number [math]\displaystyle{ x }[/math] that solves the equation [math]\displaystyle{ (x+1)^2=-9 }[/math]. To solve this problem, mathematicians introduced a symbol i (I representing the square root of -1) and called it the imaginary unit.[1] This is the imaginary number that will give −1 when it is squared.
The first mathematicians to have thought of this were probably Gerolamo Cardano and Rafael Bombelli. They lived in the 16th century.[2] It was probably Leonhard Euler who introduced writing [math]\displaystyle{ \mathrm i }[/math] for that number.
All complex numbers can be written as [math]\displaystyle{ a + bi }[/math][3] (or [math]\displaystyle{ a + b \cdot i }[/math]), where a is called the real part of the number, and b is called the imaginary part. We write [math]\displaystyle{ \Re (z) }[/math] or [math]\displaystyle{ \operatorname{Re}(z) }[/math] for the real part of a complex number [math]\displaystyle{ z }[/math]. So, if [math]\displaystyle{ z = a + bi }[/math], we write [math]\displaystyle{ a = \Re (z) = \operatorname{Re} (z) }[/math]. Similarly, we write [math]\displaystyle{ \Im (z) }[/math] or [math]\displaystyle{ \operatorname{Im} (z) }[/math] for the imaginary part of a complex number [math]\displaystyle{ z }[/math]; [math]\displaystyle{ b = \Im (z) = \operatorname{Im} (z) }[/math], for the same z.[1] Every real number is also a complex number; it is a complex number z with [math]\displaystyle{ \Im (z) = 0 }[/math].
A complex number can also be written as an ordered pair [math]\displaystyle{ (a,b) }[/math], where both a and b are real numbers. Any real number can simply be written as [math]\displaystyle{ a + 0 \cdot i }[/math], or as the pair [math]\displaystyle{ (a,0) }[/math].[3]
Sometimes, [math]\displaystyle{ j }[/math] is written instead of [math]\displaystyle{ i }[/math]. In electrical engineering for instance, [math]\displaystyle{ i }[/math] means electric current so j is used instead of [math]\displaystyle{ i }[/math], to avoid confusion as some complex numbers are often utilised in electrical engineering.
Operations over complex numbers
Addition, subtraction, multiplication and exponentiation (raising numbers to exponents) are all possible with complex numbers. Division is also possible with complex numbers, as long as the divisor is not zero. Some other calculations are also possible with complex numbers.
The rule for addition and subtraction of complex numbers is pretty simple:
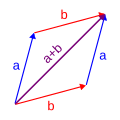
Let [math]\displaystyle{ z = (a + bi), w = (c + di) }[/math], then [math]\displaystyle{ z + w = (a + bi) + (c + di) = (a + c) + (b + d)i }[/math], and [math]\displaystyle{ z - w = (a + bi) - (c + di) = (a - c) + (b - d)i }[/math].
Multiplication is a bit different:
[math]\displaystyle{ z \cdot w = (a + bi)(c + di) = ac + bci + adi + bdi^2 = (ac - bd) + (bc + ad)i. }[/math]
Another notable operation for complex numbers is conjugation. A complex conjugate [math]\displaystyle{ \overline{z} }[/math] to [math]\displaystyle{ z = a + bi }[/math] is [math]\displaystyle{ a - bi }[/math]. It is pretty simple, but is important for calculations, because [math]\displaystyle{ z \times \overline{z} }[/math] is actually a real number for all complex [math]\displaystyle{ z }[/math]:
[math]\displaystyle{ z\bar{z}=(a+bi)(a-bi)=(a^2+b^2)+(ab-ab)i=a^2+b^2 }[/math].
Because of that, we can use it to do division:
[math]\displaystyle{ \frac{1}{z}=\frac{\bar{z}}{z\bar{z}}=\frac{a-bi}{a^2+b^2}=\frac{a}{a^2+b^2}-\frac{b}{a^2+b^2}i }[/math]
[math]\displaystyle{ \frac {w}{z}= w(\frac {1}{z})= (c+di)\cdot \left(\frac{a}{a^2+b^2} -\frac{b}{a^2+b^2}i\right)= \frac{1}{a^2+b^2}\left((cx+dy)+(dx-cy)i\right). }[/math]
Other forms of describing complex numbers
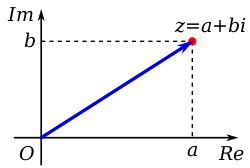
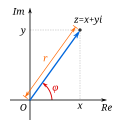
Complex numbers can be shown on a so-called complex plane. If you have a number [math]\displaystyle{ z = a + bi }[/math], you can go to point a on the real axis and point b on the imaginary axis, and draw a vector from [math]\displaystyle{ (0, 0) }[/math] to [math]\displaystyle{ (a, b) }[/math]. The length of this vector can be calculated using the Pythagorean theorem, and the angle of this vector is simply the angle between the positive real axis and this vector—going counterclockwise. The length of a vector for a number [math]\displaystyle{ z }[/math] is called its modulus or absolute value (written as [math]\displaystyle{ |z| }[/math]), and the angle is called its argument ([math]\displaystyle{ \arg z }[/math]).[1]

This leads to the trigonometrical form of describing complex numbers: by the definitions of sine and cosine, it follows that for all [math]\displaystyle{ z }[/math]:
[math]\displaystyle{ z = |z|(\cos \arg z + i \sin \arg z). }[/math]
This is closely connected to De Moivre's formula.
There exists even another form, called exponential form.
Conclusion
With the introduction of complex numbers to math, every polynomial with complex coefficients has roots in complex numbers. This introduction also helped to open a path to the creation of another kind of numbers, which could help resolve and explain many different problems. These include the hypercomplex numbers, sedenion, hyperreal numbers, surreal numbers and many others. For more, see types of numbers.
Complex Number Media
A complex number z can be visually represented as a pair of numbers (a, b) forming a position vector (blue) or a point (red) on a diagram called an Argand diagram, representing the complex plane. Re is the real axis, Im is the imaginary axis, and i is the "imaginary unit", that satisfies i2 = −1.
Multiplication of 2 + i (blue triangle) and 3 + i (red triangle). The red triangle is rotated to match the vertex of the blue one (the adding of both angles in the terms φ1+φ2 in the equation) and stretched by the length of the hypotenuse of the blue triangle (the multiplication of both radiuses, as per term r1r2 in the equation).
Euler's formula relates the complex exponential function of an imaginary argument, which can be thought of as describing uniform circular motion in the complex plane, to the cosine and sine functions, geometrically its projections onto the real and imaginary axes, respectively.
Domain coloring plot of the function*f(x) = \tfrac{(x^2 - 1)(x - 2 - i)^2}{x^2 + 2 + 2 i}*The hue represents the function argument, while the saturation and value represent the magnitude.
A domain coloring graph of the function*(z2 − 1)(z − 2 − i)2z2 + 2 + 2i. Darker spots mark moduli near zero, brighter spots are farther away from the origin. The color encodes the argument. The function has zeros for ±1, (2 + i) and poles at \pm \sqrtTemplate:-2-2i.
Related pages
References
- ↑ 1.0 1.1 1.2 1.3 "Comprehensive List of Algebra Symbols". Math Vault. 2020-03-25. Retrieved 2020-08-12.
- ↑ 2.0 2.1 "Complex Numbers | Brilliant Math & Science Wiki". brilliant.org. Retrieved 2020-08-12.
- ↑ 3.0 3.1 3.2 Weisstein, Eric. "Complex numbers". Wolfram MathWorld. Retrieved August 11, 2020.