Mass

For other uses, see Mass (disambiguation).

The mass of an object is a measure of the amount of matter it has. For example, A mountain has a greater mass than a rock. Mass is different from weight. Weight is the vector (directional) product of mass and gravitational acceleration, e.g. 9.81 ms^-2. Weight is sometimes called the force of gravity.

The mass of an object is measurable when a force is exerted on the object. If the mass is greater, the object will have less acceleration (changes in velocity), which is sometimes called inertial mass as it measures the inertia.

A gigantic mass, like our planet Earth, attracts such a smaller mass as human being to keep the human being from floating away from the Earth's surface. "Mass attraction" is another word for gravity, a force existing between all matters. When measuring the force of gravity exerted on an object, its gravitational mass can be found. Tests of inertial and gravitational mass show that they are the same or almost the same.

Units of mass

The unit of mass in the International System of Units is the kilogram, which is represented by the symbol 'kg'. Fractions and multiples of this basic unit include the gram (one thousandth of a kg, symbol 'g') and the tonne (one thousand kg), amongst many others.

In some fields or applications, it is convenient to use different units to simplify the discussions or writings. For instance,

• Atomic physicists deal with the tiny masses of individual atoms and measure them in atomic mass units.
• Jewelers normally work with small jewels and precious stones where masses are traditionally measured in carats, which correspond to 200 mg or 0.2 g.
• The masses of stars are very large and are sometimes expressed in units of solar masses.

Traditional units are still in encountered in some countries: imperial units such as the ounce or the pound were in widespread use within the British Empire. Some of them are still popular in the United States, which also uses units like the short ton (2,000 pounds, 907 kg) and the long ton (2,240 pounds, 1010 kg), not to be confused with the metric ton (1,000 kg).

Mass Media

• SI base unit.svg

  The kilogram is one of the seven SI base units.

• Mass versus weight in earth and mars.svg

  Mass and weight of a given object on Earth and Mars. Weight varies due to different amount of gravitational acceleration whereas mass stays the same.

• Apollo 15 feather and hammer drop.ogv

  Astronaut David Scott performs the feather and hammer drop experiment on the Moon.

• 

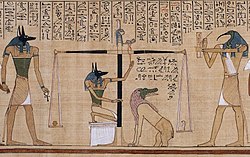
  Depiction of early balance scales in the Papyrus of Hunefer (dated to the 19th dynasty, c. 1285 BCE). The scene shows Anubis weighing the heart of Hunefer.

• Galileo.arp.300pix.jpg

  Galileo.arp.pix

• Falling ball.jpg

  Distance traveled by a freely falling ball is proportional to the square of the elapsed time.

• GodfreyKneller-IsaacNewton-1689.jpg

  Portrait of Isaac Newton (1642-1727). This is a copy of a painting by Sir Godfrey Kneller (1689).

• Newton Cannon.svg

  A cannon on top of a very high mountain shoots a cannonball horizontally. If the speed is low, the cannonball quickly falls back to Earth (A, B). At intermediate speeds, it will revolve around Earth along an elliptical orbit (C, D). Beyond the escape velocity, it will leave the Earth without returning (E).

• Universal gravitational mass.jpg

  Universal gravitational mass

• Cavendish Experiment.png

  Vertical section drawing of Cavendish's torsion balance instrument including the building in which it was housed. The large balls were hung from a frame so they could be rotated into position next to the small balls by a pulley from outside. Figure 1 of Cavendish's paper.

Main page: Conservation of mass

Mass is an intrinsic property of the object: it does not depend on its volume, or position in space, for instance. For a long time (at least since the works of Antoine Lavoisier in the second half of the eighteen century), it has been known that the sum of the masses of objects that interact or of the chemicals that react remain conserved throughout these processes. This remains an excellent approximation for everyday life and even most laboratory work.

However, Einstein has shown through his special theory of relativity that the mass m of an object moving at speed v with respect to an observer must be higher than the mass of the same object observed at rest m₀ with respect to the observer. The applicable formula is

[math]\displaystyle{ m=\frac{m_0}{\sqrt{1 - (v^2/c^2)}} }[/math]

where c stands for the speed of light. This change in mass is only important when the speed of the object with respect to the observer becomes a large fraction of c.

The Quantum Concept of Mass

For further reference,see the Gluon field and Higgs boson

In atomic nuclei, example in protons and neutrons,the residual mass comes from the binding kinetic and potential energy of the quarks and gluon field. An analogy to go along with is to think of the 3 quarks as balls with the gluons as a spring connecting the quarks. This mass accounts for 99% of the mass of these baryons with the remaining 1% coming from the individual quarks which comes from quantum interactions with the Higgs field.

Error creating thumbnail:

The Quark Structure of the proton. Most hadronic/baryonic mass comes from the binding energy (kinetic&potential) of the gluon field (with the gluons represented as springs binding the quarks.)

Error creating thumbnail:

The ATLAS detection of the mass giving Higgs Boson. The Higgs field gives elementary particles their mass and the corresponding field can be thought of as an infinite source of weak hypercharge and mass.

Related pages

• Mass versus weight
• Center of mass
• Gravity
• Density
• Body mass index
• Momentum
• Advanced topics:
  • Standard Model
  • Higgs field.