Parabola
A parabola is a type of curve. Menaechmus (380–320 BC) discovered the parabola, and Apollonius of Perga (262 BC–c190 BC) first named it.
A parabola is a conic section. If a cone is cut by a plane which is parallel to one of the surfaces of the cone, the result is a parabola.
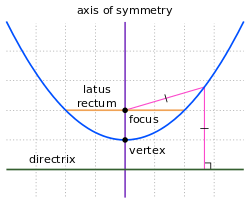
The point where the parabola reaches its maximum or minimum is called the "vertex." At this point the curvature of the parabola is greatest. This means the curve of the parabola is the tightest. The vertical line which passes through a parabola's vertex is called the "axis of symmetry". This is because the parabola looks the same on either side of that line.
Each parabola has a focal point. Any ray that enters the parabola and is parallel to the axis of symmetry will pass through this point after being reflected by the curve. Because of this fact, parabolas are important in devices such as satellite dishes, or magnifying mirrors. Parabolas are often used to approximate curves that are more difficult to model by themselves.
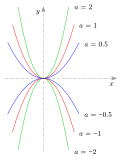
Every parabola uses the equation [math]\displaystyle{ y = ax^2 + bx + c }[/math], where [math]\displaystyle{ a }[/math], [math]\displaystyle{ b }[/math] and [math]\displaystyle{ c }[/math] are constants, and [math]\displaystyle{ a }[/math] is not equal to [math]\displaystyle{ 0 }[/math].
The bouncing of a ball will be parabolic, if the force of friction is ignored
The course of the water in a fountain is parabolic
The Gateway Arch in St. Louis looks like it is shaped like a parabola, but it is actually an inverted weighted catenary
A satellite receiver is shaped like a parabola
Parabola Media
Part of a parabola (blue), with various features (other colours). The complete parabola has no endpoints. In this orientation, it extends infinitely to the left, right, and upward.
Parabolic compass designed by Leonardo da Vinci
Parabola: general position
- Parabelnvars
When the parabola \color{blue}{y = 2x^2} is uniformly scaled by factor 2, the result is the parabola \color{red}{y = x^2}
Pencil of conics with a common vertex
Pencil of conics with a common focus
Reflective property of a parabola
