Polar coordinate system

Points in the polar coordinate system with pole O and polar axis L. In green, the point with radial coordinate 3 and angular coordinate 60 degrees or (3,60°). In blue, the point (4,210°).

In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction.

The polar coordinate system is especially useful in situations where the relationship between two points is most easily expressed with angles and distance; in the more familiar Cartesian or rectangular coordinate system, such a relationship can only be found through trigonometric formulae.

As the coordinate system is two-dimensional, each point is determined by two polar coordinates: the radial coordinate and the angular coordinate. The radial coordinate (usually denoted as [math]\displaystyle{ r }[/math]) denotes the point's distance from a central point known as the pole (equivalent to the origin in the Cartesian system). The angular coordinate (also known as the polar angle or the azimuth angle, and usually denoted by θ or [math]\displaystyle{ t }[/math]) denotes the positive or anticlockwise (counterclockwise) angle required to reach the point from the 0° ray or polar axis (which is equivalent to the positive x-axis in the Cartesian coordinate plane).^[1]

History

A polar grid with several angles labeled in degrees

The concepts of angle and radius were already used by ancient peoples of the 1st millennium BCE. Hipparchus (190-120 BCE) created a table of chord functions giving the length of the chord for each angle, and there are references to his using polar coordinates in establishing stellar positions.^[2] In On Spirals, Archimedes describes the Archimedean spiral, a function whose radius depends on the angle. The Greek work, however, did not extend to a full coordinate system.

There are various accounts of the introduction of polar coordinates as part of a formal coordinate system. The full history of the subject is described in Harvard professor Julian Lowell Coolidge's Origin of Polar Coordinates.^[3] Grégoire de Saint-Vincent and Bonaventura Cavalieri independently introduced the concepts in the mid-seventeenth century. Saint-Vincent wrote about them privately in 1625 and published his work in 1647, while Cavalieri published his in 1635 with a corrected version appearing in 1653. Cavalieri first used polar coordinates to solve a problem relating to the area within an Archimedean spiral. Blaise Pascal subsequently used polar coordinates to calculate the length of parabolic arcs.

In Method of Fluxions (written 1671, published 1736), Sir Isaac Newton examined the transformations between polar coordinates, which he referred to as the "Seventh Manner; For Spirals", and nine other coordinate systems.^[4] In the journal Acta Eruditorum (1691), Jacob Bernoulli used a system with a point on a line, called the pole and polar axis respectively. Coordinates were specified by the distance from the pole and the angle from the polar axis. Bernoulli's work extended to finding the radius of curvature of curves expressed in these coordinates.

The actual term polar coordinates has been attributed to Gregorio Fontana and was used by 18th-century Italian writers. The term appeared in English in George Peacock's 1816 translation of Lacroix's Differential and Integral Calculus.^[5]^[6] Alexis Clairaut was the first to think of polar coordinates in three dimensions, and Leonhard Euler was the first to actually develop them.^[3]

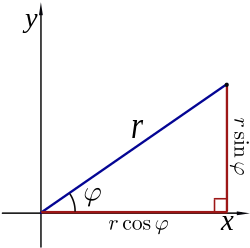
Converting between polar and Cartesian coordinates

A diagram illustrating the relationship between polar and Cartesian coordinates.

The polar coordinates r and φ can be converted to the Cartesian coordinates x and y by using the trigonometric functions sine and cosine:

[math]\displaystyle{ \begin{align} x &= r \cos \varphi, \\ y &= r \sin \varphi. \end{align} }[/math]

The Cartesian coordinates x and y can be converted to polar coordinates r and φ with r ≥ 0 and φ in the interval (− $π$ , $π$ ] by:^[7]

[math]\displaystyle{ r = \sqrt{x^2 + y^2} \quad }[/math] (as in the Pythagorean theorem.

Cylindrical coordinates

Cylindrical coordinates take the same idea that polar coordinates use, but they extend it further. To get a third dimension, each point also has a height above the original coordinate system. Each point is uniquely identified by a distance to the origin, called r here, an angle, called [math]\displaystyle{ \phi }[/math] (phi), and a height above the plane of the coordinate system, called Z in the picture.

Spherical coordinates

The same idea as is used by polar coordinates can also be extended in a different way. Instead of using two distances, and one angle only, it is possible to use one distance only, and two angles, called [math]\displaystyle{ \phi }[/math] and [math]\displaystyle{ \theta }[/math] (theta).

Polar Coordinate System Media

Hipparchos 1.jpeg

Hipparchos
An illustration of a complex number z plotted on the complex plane
An illustration of a complex number plotted on the complex plane using Euler's formula
A curve on the Cartesian plane can be mapped into polar coordinates. In this animation, y = \sin (6\!\cdot\!x) + 2 is mapped onto r = \sin (6\!\cdot\!\theta) + 2. Click on image for details.
A circle with equation $r (φ) = 1$
A polar rose with equation $r (φ) = 2 sin 4 φ$
One arm of an Archimedean spiral with equation $r (φ) = φ / 2 π$ for $0 < φ < 6 π pi$