Regular polytope

A dodecahedron, one of the five Platonic solids

In mathematics, a regular polytope is a shape with sides and vertices that are symmetrical. Like other polytopes, regular polytopes are found in any number of dimensions.

A two-dimensional regular polytope is a regular polygon, and a three-dimensional regular polytope is a regular polyhedron. Even though these groups include different shapes, they are based on the same idea of the shapes having regular symmetry. Regular polytopes have regular facets (faces, as seen from the 3D viewpoint), and their vertex figures are regular.

Each number of dimensions has a different set of regular polytopes. However, all of them have a simple shape. The simplest of regular polytopes is the triangle in 2D, the tetrahedron in 3D, and the pentachoron in 4D.

v t e Fundamental convex regular and uniform polytopes in dimensions 2–10
Family	A_n	B_n	I₂(p) / D_n	E₆ / E₇ / E₈ / F₄ / G₂	H_n
Regular polygon	Triangle	Square	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform 4-polytope	5-cell	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	1₂₂ • 2₂₁
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	1₃₂ • 2₃₁ • 3₂₁
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	1₄₂ • 2₄₁ • 4₂₁
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1_k2 • 2_k1 • k₂₁	n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds

Regular Polytope Media

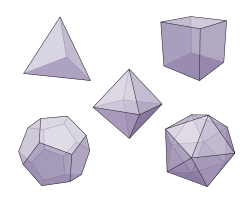
The Platonic solids. Top left to right: tetrahedron and cube. Middle: regular octahedron. Bottom left to right: dodecahedron and icosahedron.
Left to right: small stellated dodecahedron, great icosahedron, great dodecahedron, great stellated dodecahedron
A three-dimensional projection of a rotating tesseract. This tesseract is initially oriented so that all edges are parallel to one of the four coordinate space axes. The rotation takes place in the xw -plane.
The Hemicube is derived from a cube by equating opposite vertices, edges, and faces. It has 4 vertices, 6 edges, and 3 faces.
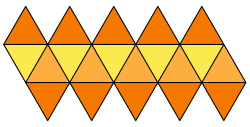
Net for icosahedron
Net for tesseract
A perspective projection (Schlegel diagram) for tesseract
An animated cut-away cross-section of the 24-cell.
A regular dodecahedral honeycomb, {5,3,4}, of hyperbolic space projected into 3-space.