Mean

In mathematics and statistics, the mean is a kind of average. Besides the mean, there are other kinds of average, and there are also a few kinds of mean. While arithmetic mean is the most commonly used mean, there are various other means and they are calculated differently. It is important to know the difference as many websites and authors have got this wrong.

Mean of some values under an operations can be thought of as the value by which we can replace all the previous values and still get the same accumulation over the operation. Here, operation is important as it determines the way accumulation is calculated and in turn what kind of mean is the actual representative of the problem at the hand.

For example, if the operation is addition, then the mean would be arithmetic mean, if the operation is product then the mean would be the geometric mean, and so on.

Arithmetic mean is calculated by adding all of the values together, then dividing by the number of values. For example, if 1, 2, 2, 100, 100 is a set of numbers or scores. If we add all the numbers, the answer is 205. By dividing this number by the number of numbers (5), we find that the mean is 41. The difficulty with this particular set of numbers is that no one in this group scored anything like a 41, and it does not tell us much about what kind of scores these numbers represent.

Calculation details

In general, to find the average of [math]\displaystyle{ N }[/math] numbers, the [math]\displaystyle{ N }[/math] numbers are added and the total is divided by [math]\displaystyle{ N }[/math].

In symbols, if the numbers are [math]\displaystyle{ X_1 }[/math], [math]\displaystyle{ X_2 }[/math], [math]\displaystyle{ X_3 }[/math], ... [math]\displaystyle{ X_N }[/math], the total is:

[math]\displaystyle{ X_1 + X_2 + X_3 + ... + X_N }[/math]

The total is divided by [math]\displaystyle{ N }[/math] to make the average:

[math]\displaystyle{ {X_1 + X_2 + X_3 + ... + X_N} \over N }[/math]

If [math]\displaystyle{ X_1 }[/math], [math]\displaystyle{ X_2 }[/math], [math]\displaystyle{ X_3 }[/math], ..., [math]\displaystyle{ X_N }[/math] are all the numbers in a sample [math]\displaystyle{ X }[/math], then this average is also called the sample mean of [math]\displaystyle{ X }[/math], and represented by the symbol [math]\displaystyle{ \overline{X} }[/math].

Examples

• Lucy is 5 years old. Tom is 6 years old. Emily is 7 years old. To find the average age:
  • Add the three numbers :

[math]\displaystyle{ 5+6+7=18 }[/math]

• The total is 18. Divide the total 18 by three:

[math]\displaystyle{ 18/3=6 }[/math]

• The average of the three numbers is 6.

[math]\displaystyle{ \frac{5+6+7}{3} }[/math]

Therefore, the average age of Lucy, Tom and Emily is 6 years.

Related calculations

The idea behind the mean is to represent a number of measurements, or values, by one value only. But there are different ways to calculate such a representing value.

• The median is the number that divides all the samples in such a way that half of the samples are below it, and the other half above. Example: 1, 10, 50, 100, 100 is a set of numbers or scores. If we look at these scores, we discover that the number 50 falls in the middle of the range of numbers, which tells us that half the numbers or scores are above this number, and half the numbers and scores are below this number. This is more information, depending on what you are trying to find out about this group of numbers, to help you find out what you want to know. It is not always possible to make the higher and lower group each exactly half of the total (for example, the equal division fails for the list 1, 2, 2).

• The modus or mode is the number that occurs most often. Example: 1, 2, 2, 100, 200 is a set of numbers or scores. If we look at the numbers we discover that the number 2 recurs most often and would tell us that the number or score of 2 is the most common score or number in the group.

• The arithmetic mean is just the average, the value that is the sum of all values, divided by their number. This is what is most often referred to as mean.

• The geometric mean is the root of the product of all values. For example, the geometric mean of 4, 6, and 9 is 6, because 4 times 6 times 9 is 216, and the cube root (because there are three values) of 216 is 6.

• The harmonic mean is the reciprocal of the arithmetic mean of the reciprocals. It is often used when people want a mean of rates or percentages.

• The root mean square (or quadratic mean) is the square root of the arithmetic mean of the squares of the values. The root mean square is at least as high as the arithmetic mean, and usually higher.

If people do many different measurements, they will get many different results. Those results have a certain distribution, and they can also be centered around an average value. This average value is what mathematicians call arithmetic mean.

Mean can also stand for expected value. For a random variable [math]\displaystyle{ X }[/math], this is represented by the symbol [math]\displaystyle{ E(X) }[/math].

Mean Media

• 

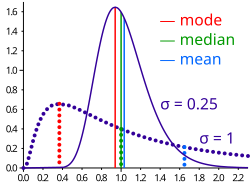
  Comparison of the arithmetic mean, median, and mode of two skewed (log-normal) distributions

• 

  Geometric visualization of the mode, median and mean of an arbitrary probability density function

Related pages

• Standard deviation