Circle

A Circle

A circle, also known as a nought, is a round, two-dimensional shape. All points on the edge of the circle are at the same distance from the center.

The radius of a circle is a line from the center of the circle to a point on the side. Mathematicians use the letter [math]\displaystyle{ r }[/math] for the length of a circle's radius. The center of a circle is the point in the very middle. It is often written as [math]\displaystyle{ O }[/math].

The diameter (meaning "all the way across") of a circle is a straight line that goes from one side to the opposite and right through the center of the circle. Mathematicians use the letter [math]\displaystyle{ d }[/math] for the length of this line. The diameter of a circle is equal to twice its radius ([math]\displaystyle{ d }[/math] equals [math]\displaystyle{ 2 }[/math] times [math]\displaystyle{ r }[/math]):

[math]\displaystyle{ d=2r }[/math]

The circumference (meaning "all the way around") of a circle is the line that goes around the center of the circle. Mathematicians use the letter [math]\displaystyle{ c }[/math] for the length of this line.

The number [math]\displaystyle{ \pi }[/math] (written as the Greek letter pi) is a very useful number. It is the length of the circumference divided by the length of the diameter ([math]\displaystyle{ \pi }[/math] equals [math]\displaystyle{ c }[/math] divided by [math]\displaystyle{ d }[/math]). As a fraction the number [math]\displaystyle{ \pi }[/math] is equal to about [math]\displaystyle{ \frac{22}{7} }[/math] or [math]\displaystyle{ \frac{355}{113} }[/math] (which is closer) and as a number it is about [math]\displaystyle{ 3.1415926536 }[/math].

	[math]\displaystyle{ \pi=\frac cd }[/math]
[math]\displaystyle{ \therefore\textrm{(therefore)} }[/math]	[math]\displaystyle{ c=2\pi r }[/math]
	[math]\displaystyle{ c=\pi d }[/math]

The area of the circle is equal to [math]\displaystyle{ \pi }[/math] times the area of the gray square.

The area, [math]\displaystyle{ A }[/math], inside a circle is equal to the radius multiplied by itself, then multiplied by [math]\displaystyle{ \pi }[/math] ([math]\displaystyle{ A }[/math] equals [math]\displaystyle{ \pi }[/math] times [math]\displaystyle{ r }[/math] times [math]\displaystyle{ r }[/math]).

[math]\displaystyle{ A=\pi r^2 }[/math]

Calculating π

[math]\displaystyle{ \pi }[/math] can be measured by drawing a circle, then measuring its diameter ([math]\displaystyle{ d }[/math]) and circumference ([math]\displaystyle{ c }[/math]). This is because the circumference of a circle is always equal to [math]\displaystyle{ \pi }[/math] times its diameter.

[math]\displaystyle{ \pi=\frac cd }[/math]

[math]\displaystyle{ \pi }[/math] can also be calculated by only using mathematical methods. Most methods used for calculating the value of [math]\displaystyle{ \pi }[/math] have desirable mathematical properties. However, they are hard to understand without knowing trigonometry and calculus. However, some methods are quite simple, such as this form of the Gregory-Leibniz series:

[math]\displaystyle{ \pi=\frac41-\frac43+\frac45-\frac47+\frac49-\frac{4}{11}+\cdots }[/math]

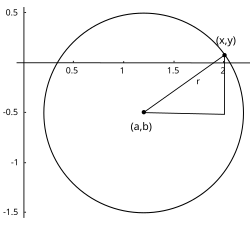
While that series is easy to write and calculate, it is not easy to see why it equals [math]\displaystyle{ \pi }[/math]. A much easier way to approach is to draw an imaginary circle of radius [math]\displaystyle{ r }[/math] centered at the origin. Then any point [math]\displaystyle{ (x,y) }[/math] whose distance [math]\displaystyle{ d }[/math] from the origin is less than [math]\displaystyle{ r }[/math], calculated by the Pythagorean theorem, will be inside the circle:

[math]\displaystyle{ d=\sqrt{x^2+y^2} }[/math]

Finding a set of points inside the circle allows the circle's area [math]\displaystyle{ A }[/math] to be estimated, for example, by using integer coordinates for a big [math]\displaystyle{ r }[/math]. Since the area [math]\displaystyle{ A }[/math] of a circle is [math]\displaystyle{ \pi }[/math] times the radius squared, [math]\displaystyle{ \pi }[/math] can be approximated by using the following formula:

[math]\displaystyle{ \pi=\frac{A}{r^2} }[/math]

Area

Using the radius: [math]\displaystyle{ A=\pi r^2=\frac{\tau r^2}{2} }[/math]

Using the diameter: [math]\displaystyle{ A=\frac{\pi d^2}{4}=\frac{\tau d^2}{8} }[/math]

Using the circumference: [math]\displaystyle{ A=\frac{c^2}{2\tau}=\frac{c^2}{4\pi} }[/math]

Circumference

Using the radius: [math]\displaystyle{ c=\tau r=2\pi r }[/math]

Using the diameter: [math]\displaystyle{ c=\pi d=\frac{\tau d}{2} }[/math]

Using the area: [math]\displaystyle{ c=\sqrt{2\tau A}=2\sqrt{\pi A} }[/math]

Diameter

Using the radius: [math]\displaystyle{ d=2r }[/math]

Using the circumference: [math]\displaystyle{ d=\frac c\pi=\frac{2c}{\tau} }[/math]

Using the area: [math]\displaystyle{ d=2\sqrt\frac A\pi=2\sqrt\frac{2A}{\tau} }[/math]

Radius

Using the diameter: [math]\displaystyle{ r=\frac d2 }[/math]

Using the circumference: [math]\displaystyle{ r=\frac c\tau=\frac{c}{2\pi} }[/math]

Using the area: [math]\displaystyle{ r=\sqrt\frac A\pi=\sqrt\frac{2A}{\tau} }[/math]

Circle Media

• 

  Chord, secant, tangent, radius, and diameter

• 

  A circle showing the arc, segment and sector

• 

  Circular cave paintings in Santa Barbara County, California

• 

  Circles in an old Arabic astronomical drawing.

• 

  Area enclosed by a circle = π × area of the shaded square

• 

  Circle of radius r = 1, centre (a, b) = (1.2, −0.5)

• 

  SecantSecantTheorem

• 

  inscribedangletheorem

• 

  The sagitta is the vertical segment.

Related pages

• Semicircle
• Sphere
• Squaring the circle
• Pi
• Tau

Other websites

• Calculate the measures of a circle online