Map projection
A map projection is a way of showing the surface of a three-dimensional sphere on a flat surface. Such projections are necessary to create maps. The problem with projections is that they change the surface in some way; this is called distortion. Depending on the purpose of the map, some distortions may be less bad. This is why cartographers use different mathematical projections for different maps.
Carl Friedrich Gauss showed that is not possible to project the surface of a sphere to a plane, without distorting it. This theorem is known as Theorema egregium today.
To understand the projections, it is easier to imagine a light source, a globe, and another geometric object. The light source shines "a shadow" of each point of the globe onto the geometric object. At the end the surface of the geometric object is unrolled, this yields the map. It is possible to tell the projections apart by the type of helper object used.
- Using a plane gives azimuthal projections.
- Using a cone gives conical projections.
- Using a cylinder gives cylindrical ones.
- Cylindrical projections "put the sphere into a cylinder, and then unroll its surface". Examples of these are Equirectangular projection, Mercator projection
- Psedocylindrincal: Same as cylindrical, but only applies to the main meridian and parallels.
Map Projection Media
An Albers projection shows areas accurately, but distorts shapes.
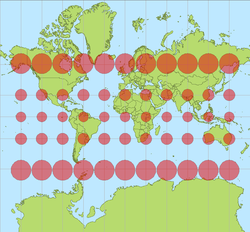
Tissot's indicatrices on the Mercator projection
A Miller cylindrical projection maps the globe onto a cylinder.
This transverse Mercator projection is mathematically the same as a standard Mercator, but oriented around a different axis.
The space-oblique Mercator projection was developed by the USGS for use in Landsat images.
The Mercator projection shows rhumbs as straight lines. A rhumb is a course of constant bearing. Bearing is the compass direction of movement.
Cylindrical equal-area projection with oblique orientation
A sinusoidal projection shows relative sizes accurately, but grossly distorts shapes. Distortion can be reduced by "interrupting" the map.
Tobler hyperelliptical projection SW
