Normal distribution
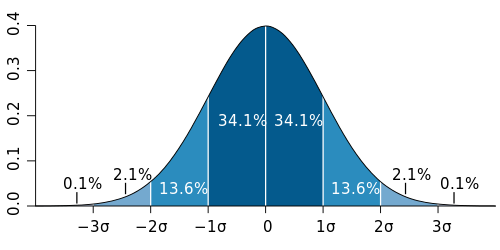
The normal distribution is a probability distribution used in probability theory and statistics. It is also called Gaussian distribution because it was first discovered by Carl Friedrich Gauss. The normal distribution is very important in many fields because many things take this form.[1] A random variable that takes this form is normally distributed, and can be called a normal deviate. The normal distribution is often called the bell curve, because the graph of its probability density looks like a bell. The standard normal distribution (also known as the Z distribution) is a normal distribution that has a mean of zero and a standard deviation of one.[2]
Probability density function The green line is the standard normal distribution | |
Cumulative distribution function Colors match the image above | |
| Parameters | [math]\displaystyle{ \mu }[/math] location (real) [math]\displaystyle{ \sigma^2\gt 0 }[/math] squared scale (real) |
|---|---|
| Support | [math]\displaystyle{ x \in\mathbb{R}\! }[/math] |
| Probability density function (pdf) | [math]\displaystyle{ \frac1{\sigma\sqrt{2\pi}}\; \exp\left(-\frac{\left(x-\mu\right)^2}{2\sigma^2} \right) \! }[/math] |
| Cumulative distribution function (cdf) | [math]\displaystyle{ \frac12 \left(1 + \mathrm{erf}\,\frac{x-\mu}{\sigma\sqrt2}\right) \! }[/math] |
| Mean | [math]\displaystyle{ \mu }[/math] |
| Median | [math]\displaystyle{ \mu }[/math] |
| Mode | [math]\displaystyle{ \mu }[/math] |
| Variance | [math]\displaystyle{ \sigma^2 }[/math] |
| Skewness | 0 |
| Excess kurtosis | 0 |
| Entropy | [math]\displaystyle{ \ln\left(\sigma\sqrt{2\,\pi\,e}\right)\! }[/math] |
| Moment-generating function (mgf) | [math]\displaystyle{ M_X(t)= \exp\left(\mu\,t+\frac{\sigma^2 t^2}{2}\right) }[/math] |
| Characteristic function | [math]\displaystyle{ \chi_X(t)=\exp\left(\mu\,i\,t-\frac{\sigma^2 t^2}{2}\right) }[/math] |
The form of the distribution is
[math]\displaystyle{ f(x) = \frac{1}{\sigma \sqrt{2\pi} } e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2} }[/math]
In a normal distribution, the parameter [math]\displaystyle{ \mu }[/math] is the mean ("average"). The standard deviation ("variability") is [math]\displaystyle{ \sigma }[/math].[2] The variance of the distribution is [math]\displaystyle{ \sigma^2 }[/math].
The normal distribution is important because it can represent real-life examples. It is used in natural and social sciences.[3][4] Some examples include:
- Height
- Test scores
- Measurement errors
- Light intensity (as in laser light)
- Insurance companies use normal distributions to model certain average cases.[5]
The central limit theorem can be used to describe real-life data as a normal distribution.[6]
Origin
Its origin goes back to the 18th century to De Moivre and in the early 19th century with Gauss.
Use
It is the most widely used piece of statistics by far. It was famously used in World War I by the United States Army to decide when men were so poor mentally that they could not be used by the Army in any job.
Normal Distribution Media
A selection of Normal Distribution Probability Density Functions (PDFs). Both the mean, μ, and variance, σ², are varied. The key is given on the graph.
A selection of Normal Distribution Cumulative Density Functions (CDFs). Both the mean, μ, and variance, σ², are varied. The key is given on the graph.
As the number of discrete events increases, the function begins to resemble a normal distribution.
Comparison of probability density functions, p(k) for the sum of n fair 6-sided dice to show their convergence to a normal distribution with increasing na, in accordance to the central limit theorem. In the bottom-right graph, smoothed profiles of the previous graphs are rescaled, superimposed and compared with a normal distribution (black curve).
The ground state of a quantum harmonic oscillator has the Gaussian distribution.
Histogram of sepal widths for Iris versicolor from Fisher's Iris flower data set, with superimposed best-fitting normal distribution
Fitted cumulative normal distribution to October rainfalls, see distribution fitting
Related pages
References
- ↑ "Normal Distribution | Data Basecamp". 2021-11-26. Retrieved 2022-07-15.
- ↑ 2.0 2.1 "List of Probability and Statistics Symbols". Math Vault. 2020-04-26. Retrieved 2020-08-15.
- ↑ "Normal Distribution - easily explained! | Data Basecamp". 2021-11-26. Retrieved 2023-05-29.
- ↑ Weisstein, Eric W. "Normal Distribution". mathworld.wolfram.com. Retrieved 2020-08-15.
- ↑ "Normal Distribution". www.mathsisfun.com. Retrieved 2020-08-15.
- ↑ Kwak, Sang Gyu; Kim, Jong Hae (2017-02-21). "Central limit theorem: the cornerstone of modern statistics". National Library of Medicine. Retrieved 2024-05-30.
Other websites
- Cumulative Area Under the Standard Normal Curve Calculator from Daniel Soper's Free Statistics Calculators website. Computes the cumulative area under the normal curve (i.e., the cumulative probability), given a z-score.
- Interactive Standard Normal Distribution
- GNU Scientific Library – Reference Manual – The Gaussian Distribution
- Normal Distribution Table
- Download free two-way normal distribution calculator
- Download free normal distribution fitting software