Surface tension
Surface tension is an effect where the surface of a liquid is strong. The surface can hold up a weight, and the surface of a water droplet holds the droplet together, in a ball shape. Some small things can float on a surface because of surface tension, even though they normally could not float. Some insects (e.g. water striders) can run on the surface of water because of this. This property is caused by the molecules in the liquid being attracted to each other (cohesion), and is responsible for many of the behaviors of liquids.
Surface tension has the dimension of force per unit length, or of energy per unit area. The two are equivalent—but when referring to energy per unit of area, people use the term surface energy—which is a more general term in the sense that it applies also to solids and not just liquids.
In materials science, surface tension is used for either surface stress or surface free energy.
Causes
The cohesive forces among the liquid molecules cause surface tension. In the bulk of the liquid, each molecule is pulled equally in every direction by neighboring liquid molecules, resulting in a net force of zero. The molecules at the surface do not have other molecules on all sides of them and therefore are pulled inwards. This creates some internal pressure and forces liquid surfaces to contract to the minimal area.
Surface tension is responsible for the shape of liquid droplets. Although easily deformed, droplets of water tend to be pulled into a spherical shape by the cohesive forces of the surface layer. In the absence of other forces, including gravity, drops of virtually all liquids would be perfectly spherical. The spherical shape minimizes the necessary "wall tension" of the surface layer according to Laplace's law.
Another way to view it is in terms of energy. A molecule in contact with a neighbor is in a lower state of energy than if it were alone (not in contact with a neighbor). The interior molecules have as many neighbors as they can possibly have, but the boundary molecules are missing neighbors (compared to interior molecules). So, the boundary molecules have a higher energy. For the liquid to minimize its energy state, the number of higher energy boundary molecules must be minimized. The minimized quantity of boundary molecules results in a minimized surface area.[1]
As a result of surface area minimization, a surface will assume the smoothest shape it can.[note 1] Any curvature in the surface shape results in greater area and a higher energy. So, the surface will push back against any curvature in much the same way as a ball pushed uphill will push back to minimize its gravitational potential energy.
Effects in everyday life
Water
Studying water shows several effects of surface tension:
A. Rain water forms beads on the surface of a waxy surface, such as a leaf. Water adheres weakly to wax and strongly to itself, so water clusters into drops. Surface tension gives them their near-spherical shape, because a sphere has the smallest possible surface area to volume ratio.
B. Formation of drops occurs when a mass of liquid is stretched. The animation shows water adhering to the faucet gaining mass until it is stretched to a point where the surface tension can no longer bind it to the faucet. It then separates and surface tension forms the drop into a sphere. If a stream of water were running from the faucet, the stream would break up into drops during its fall. Gravity stretches the stream, then surface tension pinches it into spheres.[2]
C. Objects denser than water still float when the object is nonwettable and its weight is small enough to be borne by the forces arising from surface tension.[1] For example, water striders use surface tension to walk on the surface of a pond. The surface of the water behaves like an elastic film: the insect's feet cause indentations in the water's surface, increasing its surface area.[3]
D. Separation of oil and water (in this case, water and liquid wax) is caused by a tension in the surface between dissimilar liquids. This type of surface tension is called "interface tension", but its physics are the same.
E. Tears of wine is the formation of drops and rivulets on the side of a glass containing an alcoholic beverage. Its cause is a complex interaction between the differing surface tensions of water and ethanol. It is induced by a combination of surface tension modification of water by ethanol together with ethanol evaporating faster than water.
A. Water beading on a leaf
B. Water dripping from a tap
C. Water striders stay atop the liquid because of surface tension
D. Lava lamp with interaction between dissimilar liquids; water and liquid wax
E. Photo showing the "tears of wine" phenomenon.
Surfactants
Surface tension is visible in other common phenomena, especially when surfactants are used to decrease it:
- Soap bubbles have very large surface areas with very little mass. Bubbles in pure water are unstable. The addition of surfactants, however, can have a stabilizing effect on the bubbles (see Marangoni effect). Notice that surfactants actually reduce the surface tension of water by a factor of three or more.
- Emulsions are a type of solution in which surface tension plays a role. Tiny fragments of oil suspended in pure water will spontaneously assemble themselves into much larger masses. But the presence of a surfactant provides a decrease in surface tension, which permits stability of minute droplets of oil in the bulk of water (or vice versa).
Basic physics
Two definitions
Surface tension, represented by the symbol γ is defined as the force along a line of unit length, where the force is parallel to the surface but perpendicular to the line. One way to picture this is to imagine a flat soap film bounded on one side by a taut thread of length, L. The thread will be pulled toward the interior of the film by a force equal to 2[math]\displaystyle{ \scriptstyle\gamma }[/math]L (the factor of 2 is because the soap film has two sides, hence two surfaces).[4] Surface tension is therefore measured in forces per unit length. Its SI unit is newton per meter but the cgs unit of dyne per cm is also used.[5] One dyn/cm corresponds to 0.001 N/m.
An equivalent definition, one that is useful in thermodynamics, is work done per unit area. As such, in order to increase the surface area of a mass of liquid by an amount, δA, a quantity of work, [math]\displaystyle{ \scriptstyle\gamma }[/math]δA, is needed.[4] This work is stored as potential energy. Consequently surface tension can be also measured in SI system as joules per square meter and in the cgs system as ergs per cm2. Since mechanical systems try to find a state of minimum potential energy, a free droplet of liquid naturally assumes a spherical shape, which has the minimum surface area for a given volume.
The equivalence of measurement of energy per unit area to force per unit length can be proven by dimensional analysis.[4]
Surface curvature and pressure
If no force acts normal to a tensioned surface, the surface must remain flat. But if the pressure on one side of the surface differs from pressure on the other side, the pressure difference times surface area results in a normal force. In order for the surface tension forces to cancel the force due to pressure, the surface must be curved. The diagram shows how surface curvature of a tiny patch of surface leads to a net component of surface tension forces acting normal to the center of the patch. When all the forces are balanced, the resulting equation is known as the Young–Laplace equation:[6]
- [math]\displaystyle{ \Delta p\ =\ \gamma \left( \frac{1}{R_x} + \frac{1}{R_y} \right) }[/math]
where:
- Δp is the pressure difference.
- [math]\displaystyle{ \scriptstyle\gamma }[/math] is surface tension.
- Rx and Ry are radii of curvature in each of the axes that are parallel to the surface.
The quantity in parentheses on the right hand side is in fact (twice) the mean curvature of the surface (depending on normalization).
Solutions to this equation determine the shape of water drops, puddles, menisci, soap bubbles, and all other shapes determined by surface tension. (Another example is the shape of the impressions that a water strider's feet make on the surface of a pond).
The table below shows how the internal pressure of a water droplet increases with decreasing radius. For not very small drops the effect is subtle, but the pressure difference becomes enormous when the drop sizes approach the molecular size. (In the limit of a single molecule the concept becomes meaningless.)
| Δp for water drops of different radii at STP | ||||
|---|---|---|---|---|
| Droplet radius | 1 mm | 0.1 mm | 1 μm | 10 nm |
| Δp (atm) | 0.0014 | 0.0144 | 1.436 | 143.6 |
Liquid surface
It is hard to find the shape of the minimal surface bounded by some arbitrary shaped frame using just mathematics. Yet by fashioning the frame out of wire and dipping it in soap-solution, a locally minimal surface will appear in the resulting soap-film within seconds.[4][7]
The reason for this is that the pressure difference across a fluid interface is proportional to the mean curvature, as seen in the Young-Laplace equation. For an open soap film, the pressure difference is zero, hence the mean curvature is zero, and minimal surfaces have the property of zero mean curvature.
Contact angles
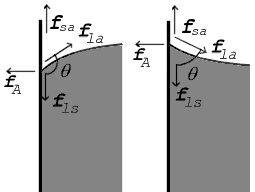
The surface of any liquid is an interface between that liquid and some other medium.[note 2] The top surface of a pond, for example, is an interface between the pond water and the air. Surface tension, then, is not a property of the liquid alone, but a property of the liquid's interface with another medium. If a liquid is in a container, then besides the liquid/air interface at its top surface, there is also an interface between the liquid and the walls of the container. The surface tension between the liquid and air is usually different (greater than) its surface tension with the walls of a container. Where the two surfaces meet, the geometry will balance all forces.[4][6]
Where the two surfaces meet, they form a contact angle, [math]\displaystyle{ \scriptstyle \theta }[/math], which is the angle the tangent to the surface makes with the solid surface. The diagram to the right shows two examples. Tension forces are shown for the liquid-air interface, the liquid-solid interface, and the solid-air interface. The example on the left is where the difference between the liquid-solid and solid-air surface tension, [math]\displaystyle{ \scriptstyle \gamma_{\mathrm{ls}} - \gamma_{\mathrm{sa}} }[/math], is less than the liquid-air surface tension, [math]\displaystyle{ \scriptstyle \gamma_{\mathrm{la}} }[/math], but is still positive, that is
- [math]\displaystyle{ \gamma_{\mathrm{la}}\ \gt \ \gamma_{\mathrm{ls}} - \gamma_{\mathrm{sa}}\ \gt \ 0 }[/math]
In the diagram, both the vertical and horizontal forces must cancel exactly at the contact point, known as equilibrium. The horizontal component of [math]\displaystyle{ \scriptstyle f_\mathrm{la} }[/math] is canceled by the adhesive force, [math]\displaystyle{ \scriptstyle f_\mathrm{A} }[/math].[4]
- [math]\displaystyle{ f_\mathrm{A}\ =\ f_\mathrm{la} \sin \theta }[/math]
The more important balance of forces, though, is in the vertical direction. The vertical component of [math]\displaystyle{ \scriptstyle f_\mathrm{la} }[/math] must exactly cancel the force, [math]\displaystyle{ \scriptstyle f_\mathrm{ls} }[/math].[4]
- [math]\displaystyle{ f_\mathrm{ls} - f_\mathrm{sa}\ =\ -f_\mathrm{la} \cos \theta }[/math]
| Liquid | Solid | Contact angle | |||
|---|---|---|---|---|---|
| water |
|
0° | |||
| ethanol | |||||
| diethyl ether | |||||
| carbon tetrachloride | |||||
| glycerol | |||||
| acetic acid | |||||
| water | paraffin wax | 107° | |||
| silver | 90° | ||||
| methyl iodide | soda-lime glass | 29° | |||
| lead glass | 30° | ||||
| fused quartz | 33° | ||||
| mercury | soda-lime glass | 140° | |||
| Some liquid-solid contact angles[4] | |||||
Since the forces are in direct proportion to their respective surface tensions, we also have:[6]
- [math]\displaystyle{ \gamma_\mathrm{ls} - \gamma_\mathrm{sa}\ =\ -\gamma_\mathrm{la} \cos \theta }[/math]
where
- [math]\displaystyle{ \scriptstyle \gamma_\mathrm{ls} }[/math] is the liquid-solid surface tension,
- [math]\displaystyle{ \scriptstyle \gamma_\mathrm{la} }[/math] is the liquid-air surface tension,
- [math]\displaystyle{ \scriptstyle \gamma_\mathrm{sa} }[/math] is the solid-air surface tension,
- [math]\displaystyle{ \scriptstyle \theta }[/math] is the contact angle, where a concave meniscus has contact angle less than 90° and a convex meniscus has contact angle of greater than 90°.[4]
This means that although the difference between the liquid-solid and solid-air surface tension, [math]\displaystyle{ \scriptstyle \gamma_\mathrm{ls} - \gamma_\mathrm{sa} }[/math], is difficult to measure directly, it can be inferred from the liquid-air surface tension, [math]\displaystyle{ \scriptstyle \gamma_\mathrm{la} }[/math], and the equilibrium contact angle, [math]\displaystyle{ \scriptstyle \theta }[/math], which is a function of the easily measurable advancing and receding contact angles (see main article contact angle).
This same relationship exists in the diagram on the right. But in this case we see that because the contact angle is less than 90°, the liquid-solid/solid-air surface tension difference must be negative:
- [math]\displaystyle{ \gamma_\mathrm{la}\ \gt \ 0\ \gt \ \gamma_\mathrm{ls} - \gamma_\mathrm{sa} }[/math]
Special contact angles
Observe that in the special case of a water-silver interface where the contact angle is equal to 90°, the liquid-solid/solid-air surface tension difference is exactly zero.
Another special case is where the contact angle is exactly 180°. Water with specially prepared Teflon approaches this.[6] Contact angle of 180° occurs when the liquid-solid surface tension is exactly equal to the liquid-air surface tension.
- [math]\displaystyle{ \gamma_{\mathrm{la}}\ =\ \gamma_{\mathrm{ls}} - \gamma_\mathrm{sa}\ \gt \ 0\qquad \theta\ =\ 180^\circ }[/math]
Methods of measurement
Because surface tension manifests itself in various effects, it offers a number of paths to its measurement. Which method is optimal depends upon the nature of the liquid being measured, the conditions under which its tension is to be measured, and the stability of its surface when it is deformed.
- Du Noüy Ring method: The traditional method used to measure surface or interfacial tension. Wetting properties of the surface or interface have little influence on this measuring technique. Maximum pull exerted on the ring by the surface is measured.[8]
- Du Noüy-Padday method: A minimized version of Du Noüy method uses a small diameter metal needle instead of a ring, in combination with a high sensitivity microbalance to record maximum pull. The advantage of this method is that very small sample volumes (down to few tens of microliters) can be measured with very high precision, without the need to correct for buoyancy (for a needle or rather, rod, with proper geometry). Further, the measurement can be performed very quickly, minimally in about 20 seconds. First commercial multichannel tensiometers [CMCeeker] were recently built based on this principle.
- Wilhelmy plate method: A universal method especially suited to check surface tension over long time intervals. A vertical plate of known perimeter is attached to a balance, and the force due to wetting is measured.[9]
- Spinning drop method: This technique is ideal for measuring low interfacial tensions. The diameter of a drop within a heavy phase is measured while both are rotated.
- Pendant drop method: Surface and interfacial tension can be measured by this technique, even at elevated temperatures and pressures. Geometry of a drop is analyzed optically. For details, see Drop.[9]
- Bubble pressure method (Jaeger's method): A measurement technique for determining surface tension at short surface ages. Maximum pressure of each bubble is measured.
- Drop volume method: A method for determining interfacial tension as a function of interface age. Liquid of one density is pumped into a second liquid of a different density and time between drops produced is measured.[10]
- Capillary rise method: The end of a capillary is immersed into the solution. The height at which the solution reaches inside the capillary is related to the surface tension by the equation discussed below.[11]
- Stalagmometric method: A method of weighting and reading a drop of liquid.
- Sessile drop method: A method for determining surface tension and density by placing a drop on a substrate and measuring the contact angle (see Sessile drop technique).[12]
- Vibrational frequency of levitated drops: The surface tension of superfluid 4He has been measured by studying the natural frequency of vibrational oscillations of drops held in the air by magnetics. This value is estimated to be 0.375 dyn/cm at T = 0° K.[13]
Effects
Liquid in a vertical tube
An old style mercury barometer consists of a vertical glass tube about 1 cm in diameter partially filled with mercury, and with a vacuum (called Torricelli's vacuum) in the unfilled volume (see diagram to the right). Notice that the mercury level at the center of the tube is higher than at the edges, making the upper surface of the mercury dome-shaped. The center of mass of the entire column of mercury would be slightly lower if the top surface of the mercury were flat over the entire crossection of the tube. But the dome-shaped top gives slightly less surface area to the entire mass of mercury. Again the two effects combine to minimize the total potential energy. Such a surface shape is known as a convex meniscus.
We consider the surface area of the entire mass of mercury, including the part of the surface that is in contact with the glass, because mercury does not adhere at all to glass. So the surface tension of the mercury acts over its entire surface area, including where it is in contact with the glass. If instead of glass, the tube were made out of copper, the situation would be very different. Mercury aggressively adheres to copper. So in a copper tube, the level of mercury at the center of the tube will be lower than at the edges (that is, it would be a concave meniscus). In a situation where the liquid adheres to the walls of its container, we consider the part of the fluid's surface area that is in contact with the container to have negative surface tension. The fluid then works to maximize the contact surface area. So in this case increasing the area in contact with the container decreases rather than increases the potential energy. That decrease is enough to compensate for the increased potential energy associated with lifting the fluid near the walls of the container.
If a tube is sufficiently narrow and the liquid adhesion to its walls is sufficiently strong, surface tension can draw liquid up the tube in a phenomenon known as capillary action. The height the column is lifted to is given by:[4]
- [math]\displaystyle{ h\ =\ \frac {2\gamma_\mathrm{la} \cos\theta}{\rho g r} }[/math]
where
- [math]\displaystyle{ \scriptstyle h }[/math] is the height the liquid is lifted,
- [math]\displaystyle{ \scriptstyle \gamma_\mathrm{la} }[/math] is the liquid-air surface tension,
- [math]\displaystyle{ \scriptstyle \rho }[/math] is the density of the liquid,
- [math]\displaystyle{ \scriptstyle r }[/math] is the radius of the capillary,
- [math]\displaystyle{ \scriptstyle g }[/math] is the acceleration due to gravity,
- [math]\displaystyle{ \scriptstyle \theta }[/math] is the angle of contact described above. If [math]\displaystyle{ \scriptstyle \theta }[/math] is greater than 90°, as with mercury in a glass container, the liquid will be depressed rather than lifted.
Puddles on a surface
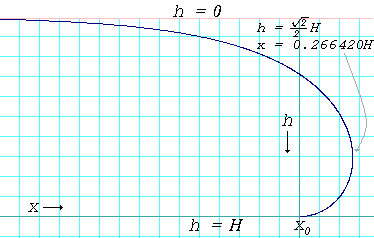
Pouring mercury onto a horizontal flat sheet of glass results in a puddle that has a perceptible thickness. The puddle will spread out only to the point where it is a little under half a centimeter thick, and no thinner. Again this is due to the action of mercury's strong surface tension. The liquid mass flattens out because that brings as much of the mercury to as low a level as possible, but the surface tension, at the same time, is acting to reduce the total surface area. The result is the compromise of a puddle of a nearly fixed thickness.
The same surface tension demonstration can be done with water, lime water or even saline, but only if the liquid does not adhere to the flat surface material. Wax is such a substance. Water poured onto a smooth, flat, horizontal wax surface, say a waxed sheet of glass, will behave similarly to the mercury poured onto glass.
The thickness of a puddle of liquid on a surface whose contact angle is 180° is given by:[6]
- [math]\displaystyle{ h\ =\ 2 \sqrt{\frac{\gamma} {g\rho}} }[/math]
where
[math]\displaystyle{ \scriptstyle h }[/math] is the depth of the puddle in centimeters or meters. [math]\displaystyle{ \scriptstyle \gamma }[/math] is the surface tension of the liquid in dynes per centimeter or newtons per meter. [math]\displaystyle{ \scriptstyle g }[/math] is the acceleration due to gravity and is equal to 980 cm/s2 or 9.8 m/s2 [math]\displaystyle{ \scriptstyle \rho }[/math] is the density of the liquid in grams per cubic centimeter or kilograms per cubic meter
In reality, the thicknesses of the puddles will be slightly less than what is predicted by the above formula because very few surfaces have a contact angle of 180° with any liquid. When the contact angle is less than 180°, the thickness is given by:[6]
- [math]\displaystyle{ h\ =\ \sqrt{\frac{2\gamma_\mathrm{la}\left( 1 - \cos \theta \right)} {g\rho}}. }[/math]
For mercury on glass, γHg = 487 dyn/cm, ρHg = 13.5 g/cm3 and θ = 140°, which gives hHg = 0.36 cm. For water on paraffin at 25 °C, γ = 72 dyn/cm, ρ = 1.0 g/cm3, and θ = 107° which gives hH2O = 0.44 cm.
The formula also predicts that when the contact angle is 0°, the liquid will spread out into a micro-thin layer over the surface. Such a surface is said to be fully wettable by the liquid.
The breakup of streams into drops
In day-to-day life we all observe that a stream of water emerging from a faucet will break up into droplets, no matter how smoothly the stream is emitted from the faucet. This is due to a phenomenon called the Plateau–Rayleigh instability,[6] which is entirely a consequence of the effects of surface tension.
The explanation of this instability begins with the existence of tiny perturbations in the stream. These are always present, no matter how smooth the stream is. If the perturbations are resolved into sinusoidal components, we find that some components grow with time while others decay with time. Among those that grow with time, some grow at faster rates than others. Whether a component decays or grows, and how fast it grows is entirely a function of its wave number (a measure of how many peaks and troughs per centimeter) and the radii of the original cylindrical stream.
Data table
| Liquid | Temperature °C | Surface tension, γ |
|---|---|---|
| Acetic acid | 20 | 27.6 |
| Acetic acid (40.1%) + Water | 30 | 40.68 |
| Acetic acid (10.0%) + Water | 30 | 54.56 |
| Acetone | 20 | 23.7 |
| Diethyl ether | 20 | 17.0 |
| Ethanol | 20 | 22.27 |
| Ethanol (40%) + Water | 25 | 29.63 |
| Ethanol (11.1%) + Water | 25 | 46.03 |
| Glycerol | 20 | 63 |
| n-Hexane | 20 | 18.4 |
| Hydrochloric acid 17.7M aqueous solution | 20 | 65.95 |
| Isopropanol | 20 | 21.7 |
| Liquid Nitrogen | -196 | 8.85 |
| Mercury | 15 | 487 |
| Methanol | 20 | 22.6 |
| n-Octane | 20 | 21.8 |
| Sodium chloride 6.0M aqueous solution | 20 | 82.55 |
| Sucrose (55%) + water | 20 | 76.45 |
| Water | 0 | 75.64 |
| Water | 25 | 71.97 |
| Water | 50 | 67.91 |
| Water | 100 | 58.85 |
Gallery of effects
Breakup of a moving sheet of water bouncing off of a spoon.
Photo of flowing water adhering to a hand. Surface tension creates the sheet of water between the flow and the hand.
Surface tension prevents a coin from sinking: the coin is indisputably denser than water, so it must be displacing a volume greater than its own for buoyancy to balance mass.
A daisy. The entirety of the flower lies below the level of the (undisturbed) free surface. The water rises smoothly around its edge. Surface tension prevents water filling the air between the petals and possibly submerging the flower.
A metal paper clip floats on water. Several can usually be carefully added without overflow of water.
An aluminium coin floats on the surface of the water at 10 °C. Any extra weight would drop the coin to the bottom.
.jpg)
Surface Tension Media
Rain water flux from a canopy. Among the forces that govern drop formation: surface tension, cohesion, Van der Waals force, Plateau–Rayleigh instability.
Surface tension and hydrophobicity interact in this attempt to cut a water droplet.
Surface tension experimental demonstration with soap
Water droplet lying on a damask. Surface tension is high enough to prevent seeping through the textile
This diagram illustrates the force necessary to increase the surface area. This force is proportional to the surface tension.
Notes
- ↑ The mathematical proof that "smooth" shapes minimize surface area relies on use of the Euler–Lagrange equation.
- ↑ In a mercury barometer, the upper liquid surface is an interface between the liquid and a vacuum containing some molecules of evaporated liquid.
References
- ↑ 1.0 1.1 1.2 White, Harvey E. (1948). Modern College Physics. van Nostrand. ISBN 0442294018.
- ↑ John W. M. Bush (May 2004). "MIT Lecture Notes on Surface Tension, lecture 5" (PDF). Massachusetts Institute of Technology. Retrieved April 1, 2007.
- ↑ John W.M. Bush (May 2004). "MIT Lecture Notes on Surface Tension, lecture 3" (PDF). Massachusetts Institute of Technology. Retrieved April 1, 2007.
- ↑ 4.0 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9 Sears, Francis Weston; Zemanski, Mark W. University Physics 2nd ed. Addison Wesley 1955
- ↑ John W.M. Bush (April 2004). "MIT Lecture Notes on Surface Tension, lecture 1" (PDF). Massachusetts Institute of Technology. Retrieved April 1, 2007.
- ↑ 6.0 6.1 6.2 6.3 6.4 6.5 6.6 6.7 Pierre-Gilles de Gennes; Françoise Brochard-Wyart; David Quéré (2002). Capillary and Wetting Phenomena—Drops, Bubbles, Pearls, Waves. Alex Reisinger. Springer. ISBN 0-387-00592-7.
- ↑ Aaronson, Scott (2005). "NP-Complete Problems and physical reality" (PDF). SIGACT News. arXiv:quant-ph/0502072. Bibcode:2005quant.ph..2072A. doi:10.1145/1052796.1052804. S2CID 18759797.
- ↑ "Surface Tension by the Ring Method (Du Nouy Method)" (PDF). PHYWE. Retrieved 2007-09-08.
- ↑ 9.0 9.1 "Surface and Interfacial Tension". Langmuir-Blodgett Instruments. Archived from the original on 2007-10-12. Retrieved 2007-09-08.
- ↑ "Surfacants at interfaces" (PDF). lauda.de. Archived from the original (PDF) on 2007-09-27. Retrieved 2007-09-08.
- ↑ Calvert, James B. "Surface Tension (physics lecture notes)". University of Denver. Retrieved 2007-09-08.
- ↑ "Sessile Drop Method". Dataphysics. Archived from the original on August 8, 2007. Retrieved 2007-09-08.
- ↑ Vicente, C.; Yao, W.; Maris, H.; Seidel, G. (2002). "Surface tension of liquid 4He as measured using the vibration modes of a levitated drop". Physical Review B. 66 (21): 214504. Bibcode:2002PhRvB..66u4504V. doi:10.1103/PhysRevB.66.214504.
- ↑ Lange's Handbook of Chemistry (1967) 10th ed. pp 1661–1665 ISBN 0070161909 (11th ed.)
Other websites
- On surface tension and interesting real-world cases
- MIT Lecture Notes on Surface Tension Archived 2007-10-27 at the Wayback Machine
- Surface Tensions of Various Liquids
- Calculation of temperature-dependent surface tensions for some common components
- Surface Tension Calculator For Aqueous Solutions Containing the Ions H+, NH4+, Na+, K+, Mg2+, Ca2+, SO42–, NO3–, Cl–, CO32–, Br– and OH–.
- The Bubble Wall[dead link] (Audio slideshow from the National High Magnetic Field Laboratory explaining cohesion, surface tension and hydrogen bonds)